Материалы зубчатых колес и допускаемые напряжения3.1.1 Назначим дешёвую углеродистую качественную конструкционную сталь 45 по ГОСТ 1050 – 88. После улучшения (закалка и высокий отпуск до окончательной обработки резанием) материал колёс должен иметь нижеследующие механические свойства /2. с.34/
Шестерня Колесо Твёрдость НВ 230…260 НВ 200…225 Предел текучести σт не менее 440 МПа 400 МПа Предел прочности σв не менее 750 МПа 690 МПа
3.1.2 Допускаемые контактные напряжения при расчете зубьев на выносливость в общем случае /2. с. 33/:
где sНlimb – предел контактной выносливости при базовом числе циклов, МПа; КHL – коэффициент долговечности; [SH] – коэффициент безопасности. Для стальных колес с твердостью менее НВ 350 /2,с.34/
Коэффициент долговечности /2,с.33/ KHL = где NНО – базовое число циклов; NНЕ – эквивалентное число циклов перемены напряжений. Для стали с твердостью НВ 200 базовое число циклов NНО = 107 /2. с.34/. Эквивалентное число циклов /3,с.184/ NНЕ = 60 × с × n × t, (3.4) где с – число зубчатых колес, сцепляющихся с данным колесом; n – частота вращения этого колеса, об/мин; t – срок службы передачи в часах.
 =60,6 об/мин. По заданию на расчетную работу срок службы составляет 10 лет при двухсменной работе. Приняв число рабочих дней в году 250, а продолжительность смены 8 часов, получим t=10∙2∙250∙8=40000 часов.
Расчет по формуле (3.4) дает для шестерни и колеса соответственно
Без вычислений по формуле (3.3) видно, что коэффициент долговечности для каждого из колес окажется меньше единицы, так как Если взять коэффициент безопасности [SH]=1,15 /2, с.33/, то расчет по формулам (3.1) и (3.2) даст допускаемые контактные напряжения для шестерни и колеса соответственно:
3.1.3 Допускаемое контактное напряжение при кратковременных перегрузках для колес из нормализованной, улучшенной и объемно закаленной стали зависит от предела текучести и вычисляется по формуле /3,с.187/
где
3.1.4 Допускаемые напряжения изгиба при проверочном расчете зубьев на выносливость вычисляется по формуле /3, с.190/
где sF limb – предел выносливости материала зубьев при отнулевом цикле, со ответствующий базовому числу циклов; КFL – коэффициент долговечности при расчете зубьев на изгиб; КF – коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья (в случае реверсивной передачи); [SF] – допускаемый коэффициент безопасности (запаса прочности).
По рекомендации /2, с.43…45/ берем: – для нормализованных и улучшенных сталей sF lim b = 1,8 НВ; – при одностороннем нагружении зубьев, принимая привод не реверсивным, КFC =1; – для стальных поковок и штамповок при твердости менее НВ 350 [SF] =1,75. Коэффициент долговечности /3, с.191/
NFO – базовое число циклов; NFE – эквивалентное число циклов.
Для колес с твердостью зубьев до и более НВ 350 величина m равна соответственно 6 и 9. Для всех сталей принимается NFO = 4 × 106. Для обоих колес NFE имеет те же численные значения, что и NНE.Оба эти значения (для шестерни -70∙107, для колеса 21∙107) больше NFO= 4 × 106. Поэтому принимается коэффициент долговечности КFL=1 /3, с.191, 192/. Расчет по формуле (3.7) дает соответственно для шестерни и колеса
Примечание – Здесь, как и при расчете [sН], взято минимальное значение твердости. 3.1.5 Допускаемое напряжение изгиба при расчете зубьев на кратковременные перегрузки при твердости менее НВ 350 /3,с.193/
Расчет по этой формуле с учетом характеристик материала (см. пункт 3.1.1) дает для шестерни и колеса соответственно
Межосевое расстояние цилиндрической зубчатой передачи из условия контактной выносливости активных поверхностей зубьев /2,с.32/
где u – передаточное число зубчатой пары; Т2=Т3 – момент на колесе (большем из колёс);
нагрузки по ширине венца;
Передаточное число u=iз=3,3 а момент Т2=Т3=412,7Н·м; Допускаемое напряжение Коэффициент ширины венца по межосевому расстоянию В итоге расчет по формуле (3.10) дает
Межосевое расстояние округляем до стандартного значения Нормальный модуль /2,с.36/ mn = (0,01…0,02) ×
Предварительно принимаем угол наклона зубьев b = 0° /2,с.37/. Тогда число зубьев шестерни:
Принимаем Z2 = 25 Тогда число зубьев колеса Zз = Z2×u = 25×3,3 =83 Уточненное значение:
Правильность вычислений подтверждается проверка:
Диаметры вершин зубьев шестерни и колеса:
Диаметры впадин зубьев
Ширина колеса: bз = yba×
Ширина шестерни: b2 = bз+5 = 80+5 = 85 мм
Коэффициент ширины шестерни по диаметру:
ybd2 = b2:d2 = 85:75 = 1,134
3.3. Проверочный расчёт прочности зубьев цилиндрической передачи 3.3.1. Расчётное контактное напряжение для цилиндрических передач /2,с.31/
где KH – коэффициент нагрузки; b – ширина колеса расчётная (наименьшая).
При такой скорости назначаем восьмую степень точности /2,с.32/. Коэффициент нагрузки при проверочном расчёте на контактную прочность
где
По рекомендациям /2, с.39,40/ назначаем следующие значения коэффициентов: – – –
Расчет по формуле (3.12) дает Ширину колеса берем в расчет минимальную и суммарную для обоих колес, т.е. в =80. Момент на колесе Т3=412,7 Н∙м. Расчет по формуле (3.11) дает
Условие прочности выполняется.
3.3.1 Расчет зубьев на контактную прочность по формуле (3.11) при кратковременных перегрузках моментом
3.3.3 Напряжение изгиба зубьев цилиндрических колёс при проверочном расчёте на выносливость вычисляются по формуле /2,с.46/
где Ft – окружная сила; KF – коэффициент нагрузки; YF – коэффициент формы зуба; Yβ – коэффициент, компенсирующий погрешности, возникающие из-за применения для косых зубьев той же расчётной схемы, что и для прямых; KFA – коэффициент, учитывающий неравномерность распределения на грузки между зубьями; b – ширина колеса, находящаяся в зацеплении, мм;
В зацеплении колёс быстроходной передачи действуют следующие силы: – окружная
– радиальная
Коэффициент нагрузки /2, с.42/
где
Примем /2,с.43/
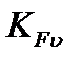 =1,25, учитывая дополнительно, что окружная скорость  =0,78 м/с, а степень точности принята 8.
Тогда по формуле (3.14) Без расчётов, руководствуясь только рекомендацией /2,с.47/, возьмём КFA=0,92. Коэффициент Yβ определим по формуле /2, с.46/:
Коэффициент формы зуба для шестерни и колеса соответственно
Расчет по формуле (3.13) дает для шестерни и колеса соответственно (в МПа):
Это значительно меньше вычисленных в пункте 3.1.4 допускаемых напряжений
3.3.4 Напряжение изгиба при кратковременных перегрузках вычисляются также по формуле (3.13) куда вместо окружной силы Ft следует подставить окружную силу при кратковременных перегрузках
После подстановки получаем при перегрузках соответственно для шестерни и колеса напряжение изгиба
 =352 МПа и  =320 МПа.
3.3.5 Геометрические параметры колес цилиндрической передачи, обоснованные в результате расчетов, сведены в таблицу 3.1.
Таблица 3.1 – Геометрические параметры колес зубчатой передачи
|
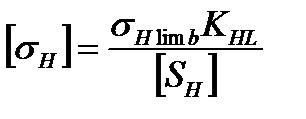, (3.1)
=2НВ+70. (3.2)
, (3.3)
> 
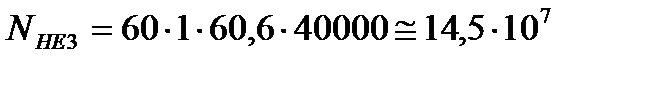
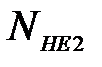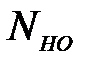и 
> 
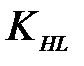=1 /2, с.33/.
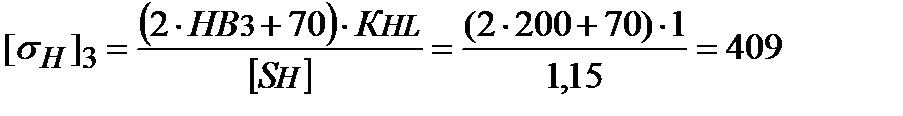МПа,
МПа,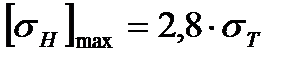
(3.6)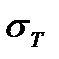
=400 МПа – предел текучести (минимальное значение для колеса по пункту 3.1.1)
МПа
(3.7)
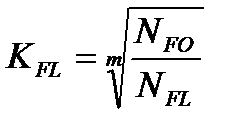
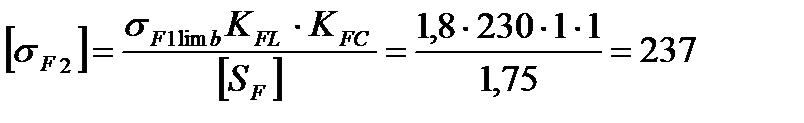МПа,
МПа.
(3.9)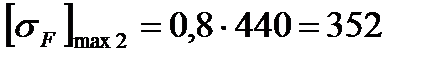
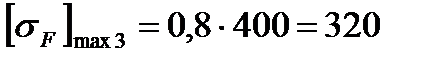МПа; 
МПа.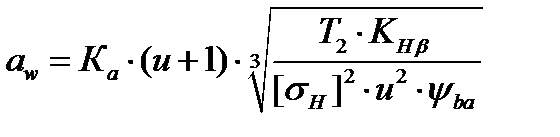
, (3.10)
– коэффициент, равный 49,5 и 43 для прямозубых и косозубых колёс соответственно;
– коэффициент, учитывающий неравномерность распределения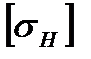
– допускаемое контактное напряжение, МПа;
– коэффициент ширины венца по межосевому расстоянию.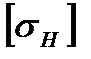
=409 МПа;
/2, с.33/Каждое из колес разделенной передачи расположено симметрично относительно опор, для этого случая примем пока ориентировочно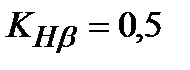 
/2,с.32/
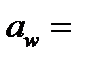160 мм /2, с.36/
= (0,01…0,02) ×160 = =1,6…3,2 мм. Из стандартного числа модулей /2,с.36/ берем mn=3 мм.
, 
.
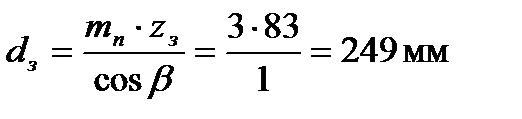
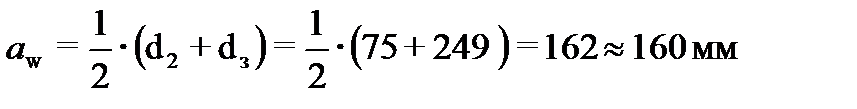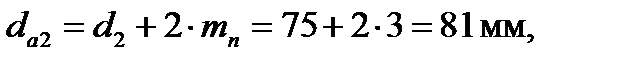
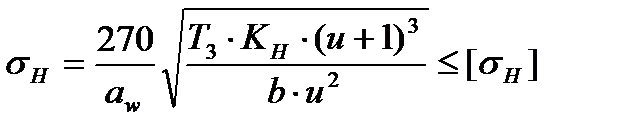, (3.11)
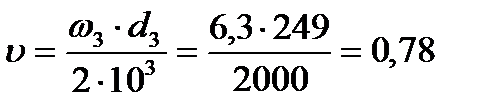м/с
(3.12)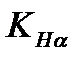
– коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;
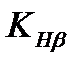– коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба;
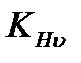– коэффициент, учитывающий дополнительные динамические нагрузки.
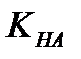= 1,при окружной скорости 
= 1,05 при значении коэффициента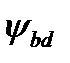 
=1,134, твёрдости зубьев менее НВ 350 и симметричном расположении относительно опор;
= 1,05 при окружной скорости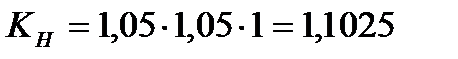 
.
МПа 
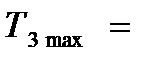854,3 Н×м дает
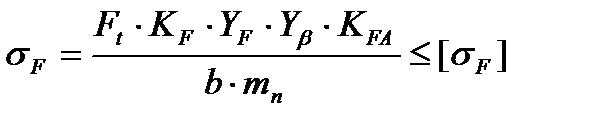(3.13)
– модуль нормальный, мм;
H;
Н;
(3.14)
– коэффициент, учитывающий неравномерность распределения нагрузки по длине зубьев;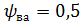
,а каждое из колес расположено симметрично относительно опор.
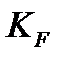=1,04·1,25=1,3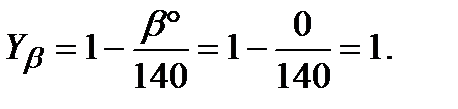
, для прямозубых колес зависит от эквивалентного числа зубьев /2,с.46/,которое составляет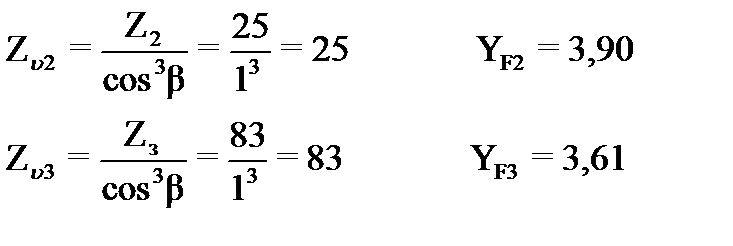
=237 МПа и 
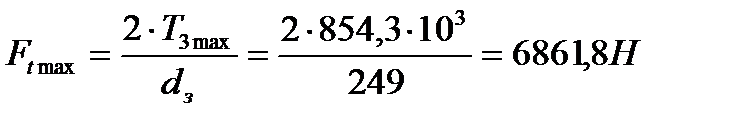
=206 МПа.
МПа
МПа
