Свободные затухающие колебания в контуре.
Всякий реальный контур обладает активным сопротивлением. Энергия, запасённая в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания затухают. Уравнение колебаний можно получить, исходя из того, что сумма падений напряжения на ёмкости, индуктивности и активном сопротивлении должна быть равна нулю:
При условии, что
где Подставляя известные значения для
Т.о. частота затухающих колебаний меньше собственной частоты Напряжение на конденсаторе:
Выражение для силы тока получим, продифференцировав по времени функцию для заряда:
Умножим и разделим это выражение на
Введя угол
Вспомнив тригонометрическую формулу: Можно записать Поскольку
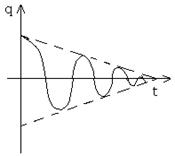
Чем больше омическое сопротивление контура, тем быстрее затухают колебания. Скорость затухания колебаний определяет коэффициент затухания Период колебаний в реальном контуре будет определяться по формуле:
Из выражений
Сопротивление контура, при котором колебательный процесс в нем переходит в непериодический, называют критическим
Величину
Чем выше добротность контура, тем медленнее в нем затухают электромагнитные колебания.
|

 преобразовав, получим:
преобразовав, получим: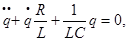 учитывая
учитывая 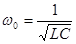 и введя обозначение
и введя обозначение 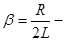 называемое коэффициентом затухания, уравнение будет иметь следующий вид:
называемое коэффициентом затухания, уравнение будет иметь следующий вид: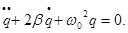 (3)
(3)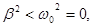 т.е.
т.е.  , тогда решение уравнения (3) будет следующее:
, тогда решение уравнения (3) будет следующее: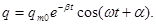
 .
. и
и  находим, что
находим, что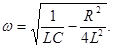
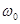 . При R=0 выражение для частоты затухающих колебаний переходит в выражение для собственной частоты.
. При R=0 выражение для частоты затухающих колебаний переходит в выражение для собственной частоты.
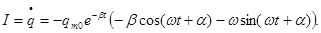
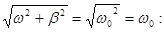

 определяемым условиями:
определяемым условиями: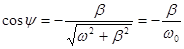 ,
, 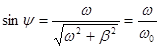 .
.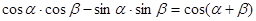 .
.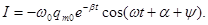
 и
и 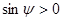 , то
, то  .
.


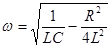 и
и 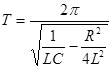 следует, что если
следует, что если  то циклическая частота
то циклическая частота  то колебания в нем не возникают.
то колебания в нем не возникают.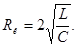
 называют волновым сопротивлением контура, а отношение волнового сопротивления контура к его активному сопротивлению – добротностью контура Q, т. е.
называют волновым сопротивлением контура, а отношение волнового сопротивления контура к его активному сопротивлению – добротностью контура Q, т. е. .
.


