Между напряжениями на отдельных участках цепи существуют углы сдвига фаз, поэтому складывать их можно только геометрически. Напряжение на входе цепи можно найти на основании второго закона Кирхгофа в векторной форме
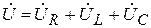 ,
,
где 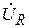 – активная составляющая напряжения катушки. Вектор
– активная составляющая напряжения катушки. Вектор 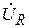 совпадает по фазе с вектором тока
совпадает по фазе с вектором тока 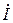 ;
;
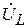 – индуктивная составляющая напряжения катушки. Вектор
– индуктивная составляющая напряжения катушки. Вектор 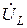 опережает вектор тока
опережает вектор тока 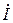 на
на 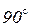 ;
;
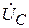 – емкостное напряжение конденсатора. Вектор
– емкостное напряжение конденсатора. Вектор 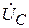 отстает от вектора тока
отстает от вектора тока 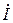 на
на 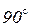 .
.
Модули этих напряжений:
 ,
, 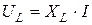 ,
, 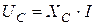 , (1)
, (1)
где  – индуктивное сопротивление катушки,
– индуктивное сопротивление катушки,
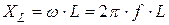 ; (2)
; (2)
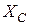 – емкостное сопротивление конденсатора,
– емкостное сопротивление конденсатора,
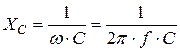 . (3)
. (3)
В формулах (2) и (3) 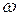 – угловая частота, а
– угловая частота, а 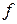 – циклическая частота входного напряжения.
– циклическая частота входного напряжения.
В зависимости от соотношения между индуктивным и емкостным сопротивлениями в цепи возможны 3 режима:
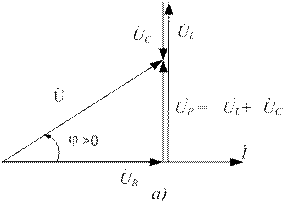
1. 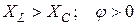 , ток в цепи отстает от приложенного к ней напряжения;
цепь носит индуктивный характер , ток в цепи отстает от приложенного к ней напряжения;
цепь носит индуктивный характер  , (рис. 2, а). , (рис. 2, а).
| 
|
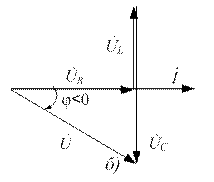
2. 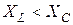 , ,  , ток в цепи опережает приложенное к ней напряжение;
цепь носит емкостный характер , ток в цепи опережает приложенное к ней напряжение;
цепь носит емкостный характер 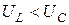 , (рис. 2, б). , (рис. 2, б).
| 
|
3. 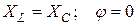 , напряжение на входе цепи совпадает по фазе с током;
цепь носит активный характер , напряжение на входе цепи совпадает по фазе с током;
цепь носит активный характер 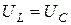 (рис. 2, в). (рис. 2, в).
|  Рис. 2. Векторные диаграммы напряжений для разных характеров цепи
Рис. 2. Векторные диаграммы напряжений для разных характеров цепи
|
Из рис. 2, а следует, что модуль напряжения на входе цепи 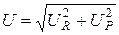 ,
,
где 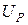 – модуль реактивного напряжения.
– модуль реактивного напряжения.
Векторы индуктивного и емкостного напряжений находятся в противофазе, поэтому модуль реактивного напряжения 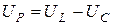 ;
;
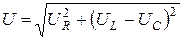 .
.
Подставив значения из формул (1) 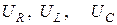 , получим:
, получим:
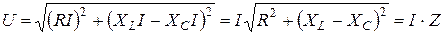 , (4)
, (4)
где 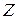 – полное сопротивление цепи переменного тока,
– полное сопротивление цепи переменного тока,
 . (5)
. (5)
Из формулы (4) получим закон Ома для цепи переменного тока: 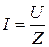 .
.
Режим, при котором в цепи с последовательным соединением индуктивного и емкостного элементов напряжение на входе совпадает по фазе с током, называется резонансом напряжений. Условием возникновения резонанса напряжений является равенство индуктивного и емкостного сопротивлений 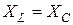 или
или  . Следовательно, режим резонанса может быть достигнут изменением индуктивности катушки
. Следовательно, режим резонанса может быть достигнут изменением индуктивности катушки 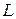 , емкости конденсатора
, емкости конденсатора 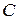 или частоты входного напряжения
или частоты входного напряжения 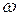 .
.
В режиме резонанса реактивное сопротивление 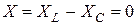 , а полное сопротивление
, а полное сопротивление 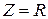 , т.е. имеет минимальное значение.
, т.е. имеет минимальное значение.

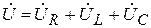 ,
,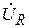 – активная составляющая напряжения катушки. Вектор
– активная составляющая напряжения катушки. Вектор 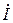 ;
;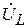 – индуктивная составляющая напряжения катушки. Вектор
– индуктивная составляющая напряжения катушки. Вектор 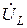 опережает вектор тока
опережает вектор тока 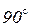 ;
;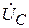 – емкостное напряжение конденсатора. Вектор
– емкостное напряжение конденсатора. Вектор  ,
, 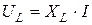 ,
, 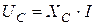 , (1)
, (1) – индуктивное сопротивление катушки,
– индуктивное сопротивление катушки,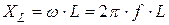 ; (2)
; (2)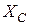 – емкостное сопротивление конденсатора,
– емкостное сопротивление конденсатора,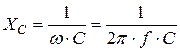 . (3)
. (3)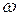 – угловая частота, а
– угловая частота, а 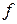 – циклическая частота входного напряжения.
– циклическая частота входного напряжения.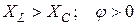 , ток в цепи отстает от приложенного к ней напряжения;
цепь носит индуктивный характер
, ток в цепи отстает от приложенного к ней напряжения;
цепь носит индуктивный характер  , (рис. 2, а).
, (рис. 2, а).

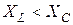 ,
,  , ток в цепи опережает приложенное к ней напряжение;
цепь носит емкостный характер
, ток в цепи опережает приложенное к ней напряжение;
цепь носит емкостный характер 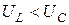 , (рис. 2, б).
, (рис. 2, б).

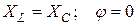 , напряжение на входе цепи совпадает по фазе с током;
цепь носит активный характер
, напряжение на входе цепи совпадает по фазе с током;
цепь носит активный характер 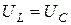 (рис. 2, в).
(рис. 2, в).
 Рис. 2. Векторные диаграммы напряжений для разных характеров цепи
Рис. 2. Векторные диаграммы напряжений для разных характеров цепи
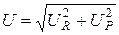 ,
,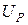 – модуль реактивного напряжения.
– модуль реактивного напряжения.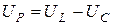 ;
;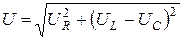 .
.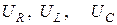 , получим:
, получим: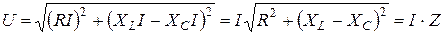 , (4)
, (4)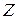 – полное сопротивление цепи переменного тока,
– полное сопротивление цепи переменного тока, . (5)
. (5)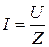 .
.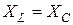 или
или  . Следовательно, режим резонанса может быть достигнут изменением индуктивности катушки
. Следовательно, режим резонанса может быть достигнут изменением индуктивности катушки 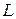 , емкости конденсатора
, емкости конденсатора 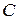 или частоты входного напряжения
или частоты входного напряжения 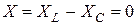 , а полное сопротивление
, а полное сопротивление 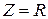 , т.е. имеет минимальное значение.
, т.е. имеет минимальное значение.


