Решение. 1. Определение степени статической неопределимости
1. Определение степени статической неопределимости Используя зависимость (14.1) подсчитаем степень статической неопределимости системы. Количество опорных стержней m =5, количество уравнений равновесия n = 3 ® 2. Выбор основной системы Известно, что основная система определяется из заданной путем отбрасывания лишних связей и приложением соответствующих усилий, возникающих в отброшенных связях в заданной системе. При этом основная система должна быть статически определимой и геометрически неизменяемой.
Рис. 17
Сравнивая три варианта основных систем (рис.17, б -17, г) приходим к выводу, что наиболее целесообразно в качестве основной системы выбрать I-ый вариант (рис. 17, б), так как в этом случае: - не требуется предварительное вычисление опорных реакций; - эпюры изгибающих моментов, построенные в этой схеме от воздействия на нее каждого из усилий Х 1 = 1, Х 2 = 1, Р и q, будут распространены на меньшем количестве участков системы и представлены простейшими геометрическими фигурами. Это значительно облегчает процесс определения коэффициентов канонических уравнений. 3. Составление системы канонических уравнений Канонические уравнения, необходимые для решения статически неопределимых задач, представляют собой уравнения совместности деформаций. Число их всегда равно степени статической неопределимости. Физический смысл каждого из канонических уравнений, как было указано выше, состоит в том, что суммарное перемещение по направлению усилий Xi от всех действующих в основной системе силовых факторов, включая и неизвестные, равно 0, так как в действительности в этих направлениях стоят связи, препятствующие возникновению перемещений по направлению этих неизвестных. Для рассматриваемого случая канонические уравнения имеют вид:
4. Вычисление коэффициентов канонических уравнений Так как все коэффициенты канонических уравнений представляют собой перемещения, то для их вычисления вначале строят единичные и грузовые эпюры изгибающих моментов в основной системе. Затем по формуле Мора с применением готовых формул (см. табл.6.1) или правила Верещагина с использованием табл.14.2 определим их значения. Эпюры изгибающих моментов, построенные в основной системе от воздействия на нее каждого в отдельности усилия X 1 = 1; X 2 = 1; P и q, показаны на рис. 17, д - 17, з. Исходя из единичных и грузовых эпюр определяем коэффициенты канонических уравнений:
5. Проверка правильности подсчета коэффициентов Правильность расчета коэффициентов канонических уравнений осуществляется путем универсальных проверок, при этом должны выполняться следующие условия:
где
Эпюра
В нашем случае
Таким образом, оба условия удовлетворяются. Следовательно, коэффициенты канонических уравнений рассчитаны верно. 6. Решение системы канонических уравнений и проверка ее правильности Подставив в систему уравнений значения коэффициентов канонических уравнений, получим:
Решив эту систему уравнений, найдем значения неизвестных: X 1 = 4,267 кН; X 2 = 0,865 кН. Правильность вычисления неизвестных проверим путем подстановки найденных значений X 1 и X 2 в исходные уравнения: 108 × 4,267 - 25,5 × 0,865 - 438,750 = 460,836 - 460,808 -25,5 × 4,267 + 11,333 × 0,865 + 99 = -108,808 + 108,803 7. Построение окончательной эпюры изгибающих моментов Mок Ординаты окончательной эпюры изгибающих моментов Mок в характерных сечениях заданной системы целесообразно подсчитать в табличной форме (табл.14.3), предварительно пронумеровав все характерные сечения и задавшись правилом знаков изгибающих моментов (рис.18, б). Окончательную эпюру изгибающих моментов Mок для заданной системы строим в соответствии с принципом независимости действия сил путем сложения «исправленных» эпюр M 1 X 1 и M 2 X 2 с грузовыми эпюрами MP и Mq, которые построены в основной системе: Mок = M 1 X 1 + M 2 X 2 + MP + Mq. «Исправленные» эпюры изгибающих моментов M 1 X 1 и M 2 X 2 строим путем умножения всех ординат единичных эпюр M 1 и M 2 , соответственно, на значения X 1 и X 2 с учетом их знака. Построенные таким образом эпюры M 1 X 1 и M 2 X 2 приведены на рис. 17, к и рис. 18, а. Таблица 14.3
Так как на участке 2-3 эпюра Mок (рис. 18, в) криволинейна, то для уточнения ее очертания необходимо найти экстремальное значение изгибающего момента. Для этого рассмотрим элемент 2-3, вырезанный из статически неопределимой системы. На этот ригель действует равномерно распределенная нагрузка q = 2 кН/м и два опорных момента М 2 = -3,128 кНм и М 3 = 5,071 кНм (табл.14.3). Расчетная схема этого элемента показана на рис. 18, г. Вначале вычислим опорные реакции, составив уравнения равновесия:
откуда R 2 = 5,733 кН и R 3 = 0,267 кН. Проверим правильность вычисления опорных реакций, составив уравнения равновесия:
Определим координату
откуда
Рис. 18
Тогда для этого сечения получим:
По найденным значениям ординат строим окончательную эпюру изгибающих моментов Мок для заданной рамы (рис. 18, в). 8. Проверка правильности построения эпюр Мок и Q(z) Для проведения статической проверки вырезаем жесткие узлы рамы кроме опорных, прикладываем все действующие в них моменты и проверяем условия равновесия В нашем примере вырежем узлы B и С (рис. 18, д) и проверим их равновесие. Узел В: Узел С: Условия равновесия узлов B и С выполняются. Выполнение условия равновесия узлов является необходимым, но недостаточным. Достаточным условием правильности определения Мок является выполнение деформационной проверки заданной системы с применением эпюры Мок, суть которого заключается в доказательстве отсутствия перемещения в точках и по направлению каждой отброшенной связи, т.е.:
Эта проверка хотя и не имеет физического смысла, так как складываются различные по направлению перемещения, но она дает возможность доказать правильность построения Мок во всех сечениях заданной системы. Для удобства вычислений целесообразно расчленить криволинейную эпюру Мок на участке рамы 2-3 (рис. 18, в) на трапецеидальную и параболическую (подобно приведенному выше на рис. 15). Тогда
Ординаты эпюры
где Участок 0-1. На этом участке внешняя нагрузка отсутствует, поэтому
Участок 2-3. В этом случае при наличии нагрузки q = 2 кН/м имеем:
откуда при z = 0: Q 2 = 5,733 кН; при z = l = 3 м: Q 3 = 5,733 - 6= -0,267 кН. Участок 4-5. Участок 6-7. Участок 8-9. По найденным значениям ординат строим эпюру Q (рис. 18, е). 9. Построение эпюры N Ординаты эпюры продольных сил определяем из условий равновесия Вырезав узел В (рис. 18, ж), составим уравнения равновесия:
Знак «минус» говорит о том, что направления продольных усилий ригеля и стойки были приняты неверно. Поэтому в действительности ригель и стойка не работают на растяжение, а на сжатие. Из рассмотрения равновесия узла С (рис. 18, з) следует:
По вычисленным значениям ординат для каждого участка строим эпюру N (рис. 18, и). 10. Статическая проверка рамы в целом Статическая проверка рамы в целом производится для подтверждения правильности построения эпюр Q, N и Мок. Она заключается в проверке равновесия рамы в целом или любой отсеченной ее части, т.е. проверке удовлетворения условий равновесия Для выполнения этой проверки отсечем заданную раму от всех опор и заменим их действие возникающими в этих сечениях внутренними усилиями Q, N и M (рис. 18, к), значения которых определяются по эпюрам Q, N и Mок . Направление всех внутренних усилий при этом должно соответствовать их знаку. Следовательно:
Уравнения равновесия удовлетворяются, cледовательно, рама рассчитана верно.
|

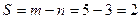 , следовательно, система дважды статически неопределима, или, другими словами, имеет две лишние связи.
, следовательно, система дважды статически неопределима, или, другими словами, имеет две лишние связи.
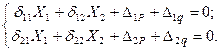 (14.16)
(14.16)
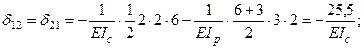
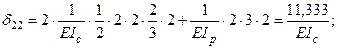
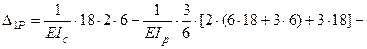
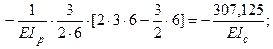
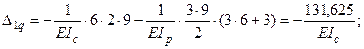
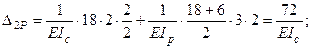
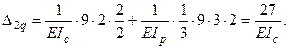
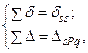
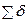 - сумма всех найденных главных и побочных коэффициентов:
- сумма всех найденных главных и побочных коэффициентов: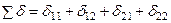 ;
;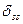 - величина, полученная в результате умножения единичной суммарной эпюры
- величина, полученная в результате умножения единичной суммарной эпюры 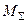 на себя:
на себя: ;
; - величина, определяемая сложением значений, полученных в результате умножения эпюры
- величина, определяемая сложением значений, полученных в результате умножения эпюры 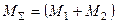 .
.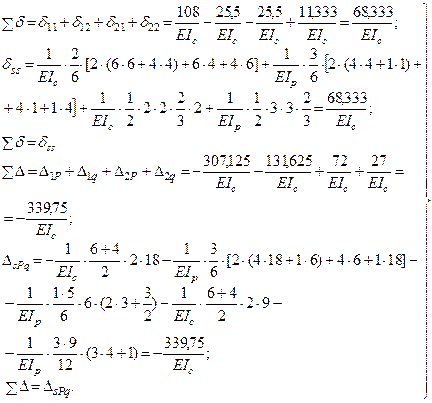

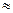 0;
0; ;
;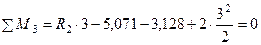 ,
,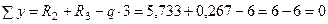 .
. сечения, в котором Q = 0, а M =
сечения, в котором Q = 0, а M = 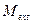 , использовав следующую дифференциальную зависимость:
, использовав следующую дифференциальную зависимость: ,
, м.
м.
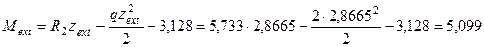 кНм.
кНм. .
.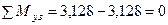 .
. .
.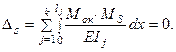
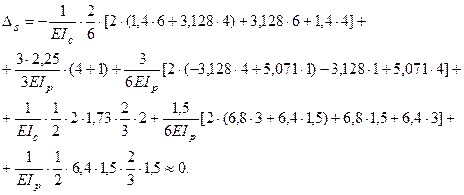
 определяем используя зависимость
определяем используя зависимость  или записывая в конечных разностях:
или записывая в конечных разностях: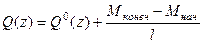 . (14.17)
. (14.17)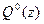 - поперечная сила в сечениях с координатой z по длине участка, имеющего расчетную схему в виде простой двухопорной балки, загруженной заданной внешней нагрузкой (рис. 18, г).
- поперечная сила в сечениях с координатой z по длине участка, имеющего расчетную схему в виде простой двухопорной балки, загруженной заданной внешней нагрузкой (рис. 18, г). , и
, и 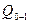 определяем по формуле (14.17):
определяем по формуле (14.17):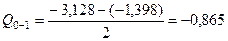 кН.
кН. ,
, кН.
кН.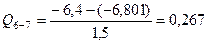 кН.
кН. кН.
кН.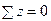 и
и  узлов рамы, вырезанных из эпюры Q. При этом отрицательную поперечную силу направляем так, чтобы она вращала вырезанный узел против хода часовой стрелки, а положительную - по ходу часовой стрелки. Нормальные силы направляем от узла, т.е. предполагаем, что стойка и ригель растянуты.
узлов рамы, вырезанных из эпюры Q. При этом отрицательную поперечную силу направляем так, чтобы она вращала вырезанный узел против хода часовой стрелки, а положительную - по ходу часовой стрелки. Нормальные силы направляем от узла, т.е. предполагаем, что стойка и ригель растянуты.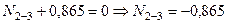 кН;
кН; кН.
кН.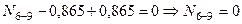 ;
;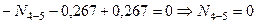 .
. под воздействием внешних нагрузок и внутренних усилий, возникающих в местах проведенных сечений.
под воздействием внешних нагрузок и внутренних усилий, возникающих в местах проведенных сечений.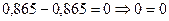 ;
; ;
;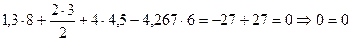 .
.


