Расчет неразрезной балки методом сил. Уравнение трех моментов
Неразрезной балкой называется статически неопределимая балка, опирающаяся в пролете на конечное число шарнирных опор. Крайние сечения неразрезной балки могут быть свободны, заделаны или шарнирно оперты. Одна из опор неразрезной балки имеет связь, препятствующую смещению балки вдоль ее оси. Расчет неразрезной балки (рис. 24, а) можно выполнить, как и любой статически неопределимой системы методом сил. Основную систему для расчета неразрезной балки получим, удалив из нее связи, препятствующие взаимному повороту смежных сечений балки над ее опорами, т.е. поместив шарниры в опорных сечениях балки (рис. 24, б).
Рис. 24
Неизвестными являются изгибающие моменты, возникающие в сечении неразрезной балки над опорами. Выделим из основной системы четыре примыкающих друг к другу пролета со средней опорой номером n и построим единичные и грузовые эпюры (рис. 25). Из анализа единичных эпюр видно, что в любом каноническом уравнении только три единичных коэффициента будут отличны от нуля. Напишем одно из канонических уравнений в общем виде:
Подсчитаем единичные и грузовые коэффициенты, применяя правило Верещагина «перемножения» эпюр:
Подставим найденные коэффициенты в (14.22), получим:
В случае балки постоянного сечения J 1 = J 2 =...= Jn = Jn +1 и введя обозначения Xn -1 = M n -1; Xn = Mn; Xn +1 = Mn+ 1, получим:
Это и есть уравнение трех моментов для неразрезной балки постоянного сечения. В этом уравнении неизвестными являются изгибающие моменты на опорах. Если у неразрезной балки все опоры шарнирные, то таких уравнений можно составить столько, сколько у балки промежуточных опор. При наличии на концах балки нагруженных консолей, изгибающие моменты на крайних опорах войдут в уравнение трех моментов, как известные величины, а при отсутствии консолей эти моменты будут равны 0. Если конец неразрезной балки защемлен, то для применения уравнения (14.25) необходимо, отбросив заделку, ввести с ее стороны дополнительный пролет
Рис. 25
Решая совместно, составленные таким образом уравнения, найдем все неизвестные изгибающие моменты на опорах. Далее для построения эпюр M и Q, каждый пролет неразрезной балки рассматриваем как балку на двух шарнирных опорах, загруженных внешней нагрузкой и двумя опорными моментами. Ординаты эпюр могут быть подсчитаны по формулам:
где Чтобы убедиться в правильности построения эпюр М и Q необходимо провести проверку равновесия неразрезной балки по уравнениям: Для этого следует определить вертикальные опорные реакции неразрезной балки, используя эпюру Q:
|


 . (14.22)
. (14.22)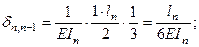


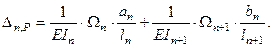 (14.23)
(14.23)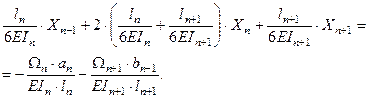 (14.24)
(14.24) . (14.25)
. (14.25)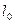 =0 (рис.25). Такая системабудет деформироваться также, как балка с жесткой заделкой.
=0 (рис.25). Такая системабудет деформироваться также, как балка с жесткой заделкой.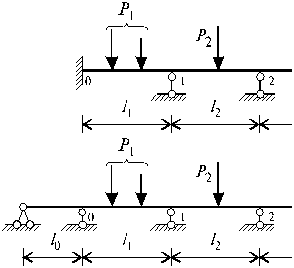
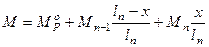 , (14.26)
, (14.26)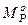 и
и  - ординаты эпюр М и Q от внешней нагрузки в основной системе.
- ординаты эпюр М и Q от внешней нагрузки в основной системе.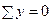 ;
; 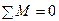 .
. . (14.27)
. (14.27)


