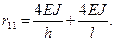Пример 1.Рассмотрим трижды статически неопределимую систему (рис. 32, а).
А) Заданная система б) Основная система в) Единичное состояние системы Рис. 32
Степень кинематической неопределимости задачи
Введём защемление узла. В результате получаем основную систему метода. Реактивный момент в левом защемлении, согласно рис. 32, а, равен:
Превратим теперь защемление в узловое и повернём узел 1 на единичный угол Согласно рис. 31, а в примыкающих к узлу стержнях на их концах возникают моменты
Подставляя значения найденных коэффициентов в каноническое уравнение (14.34), получим:
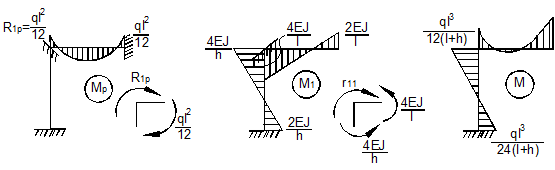
Эпюры от внешней нагрузки в основной системе и от единичного смещения показаны на рис. 33, а,б.
а) б) в) Рис. 33
Используя формулу (14.32) находим узловые моменты и строим суммарную эпюру моментов (рис. 33, в).
|
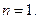Неизвестных перемещений – одно. Это поворот узла 
Каноническое уравнение метода перемещений:
(14.34)
(рис. 32, в).
и 
(рис. 33, б). Из равновесия узла находим:
