Метод перемещений
При расчёте статически неопределимых систем методом сил сначала находятся лишние неизвестные, затем внутренние силовые факторы и перемещения. Можно решить задачу раскрытия статической неопределимости иначе: сначала найти перемещения характерных точек упругой системы, а затем внутренние силовые факторы. Метод перемещений отличается от метода сил тем, что за основные неизвестные принимаются перемещения узлов стержневой системы (углы поворота и линейные перемещения). Поэтому особенно просто раскрывается статическая неопределимость системы с малым числом узлов. Стержневые деформируемые системы обладают конечным числом степеней свободы, которое совпадает с числом независимых перемещений узлов. Для плоской системы в общем случае каждый жесткий узел имеет три степени свободы (одно угловое перемещение и два линейных). Если известны перемещения узлов, то можно найти перемещения любой точки стержневой системы. Общее число неизвестных перемещений n метода перемещений, называемое степенью кинематической неопределимости, определяем как сумму неизвестных углов поворота
Число неизвестных углов поворота равно числу жестких узлов. При определении линейных смещений предполагается, что при изгибе сближением концов стержней можно пренебречь. В силу этого предположения число независимых линейных перемещений узлов равно степени свободы шарнирной схемы системы, получаемой путём введения шарниров во все узлы, включая опорные. В качестве примера рассмотрим портальную раму на рис.26.
а) б) в) Рис. 26
Внешние моменты в узлах считаем положительными при их вращении по часовой стрелке. Это же правило принимаем для углов поворота узлов. Рама три раза статически неопределима. Число жёстких узлов
а) б) Рис. 27
Усложним раму (рис.27), число узлов Рассмотрим раму (рис.26, а) и нагрузим её обобщёнными силами
решая уравнение (14.28) относительно сил
Если узловой нагрузки
или в развёрнутом виде:
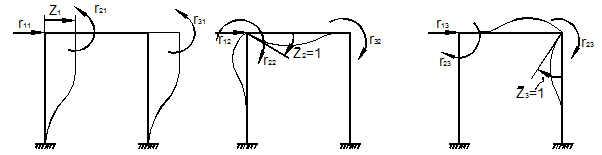
Система (14.30) называется канонической системой уравнений метода перемещений, причём Выясним статический смысл коэффициентов
а) б) в) Рис. 28
Таким образом, Аналогично выясняется смысл остальных коэффициентов жёсткости На основании теоремы о взаимности работ имеем
где
а) б) в) Рис. 29
Представим теперь, что мы наложили дополнительные связи в узлах от их поворота или линейных смещений. Тогда рама превращается в совокупность однопролётных балок с жёстко защемлёнными или шарнирно опёртыми концами (рис. 29). Такая система носит название основной системы метода перемещений. Если к основной системе приложить внешние силы (рис. 29, в), то получим систему эквивалентную заданной на основании принципа независимости действия сил. Пусть теперь внешняя нагрузка отсутствует. Будем придавать узлам основной системы единичные смещения Приложим теперь к основной системе внешнюю внутрипролётную нагрузку (рис. 29, в). Так как при этом все Методика определения коэффициентов
после интегрирования имеет вид
Рис. 30
При
Решая эту систему уравнений, находим постоянные:
Внутренние силовые факторы:
Подставляя значение постоянных, находим:
где Если правая опора шарнирная, то
а затем
а) б) Рис. 31
На рис. 31 показаны реакции Решая далее систему канонических уравнений (14.30), находим неизвестные перемещения
либо
находим изгибающие моменты в узлах рамы и строим эпюру моментов.
Примеры расчёта стержневых систем методом перемещений
|

 и неизвестных линейных перемещений
и неизвестных линейных перемещений 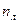 :
: .
.
 . Чтобы найти
. Чтобы найти 
 , число простых дополнительных внешних связей
, число простых дополнительных внешних связей 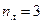 . Следовательно, число неизвестных перемещений по методу перемещений n = 9+3 = 12. По методу сил число неизвестных
. Следовательно, число неизвестных перемещений по методу перемещений n = 9+3 = 12. По методу сил число неизвестных  .
.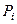 (i =1,2,…, m) в узлах и распределённой нагрузкой интенсивности
(i =1,2,…, m) в узлах и распределённой нагрузкой интенсивности 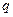 , либо сосредоточенными силами Р в пролётах такую стержневую систему называют заданной. В соответствии с законом Гука
, либо сосредоточенными силами Р в пролётах такую стержневую систему называют заданной. В соответствии с законом Гука (14.28)
(14.28) (14.29)
(14.29) (14.30)
(14.30)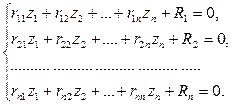

 что следует из теоремы о взаимности перемещений. При отсутствии поперечной нагрузки
что следует из теоремы о взаимности перемещений. При отсутствии поперечной нагрузки 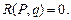
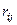 , называемых коэффициентами жёсткости. Дадим, например узлам системы (рис. 28, а) перемещения
, называемых коэффициентами жёсткости. Дадим, например узлам системы (рис. 28, а) перемещения 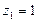 ,
, 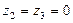 . Тогда из (14.30) следует:
. Тогда из (14.30) следует:
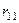 ,
,  ,
, 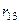 – это обобщённые силы, которые нужно приложить в узлах в направлении неизвестных перемещений, чтобы получить единичное перемещение узла
– это обобщённые силы, которые нужно приложить в узлах в направлении неизвестных перемещений, чтобы получить единичное перемещение узла 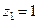 .
. , т.е. узла j. Такая трактовка справедлива только для упругих систем.
, т.е. узла j. Такая трактовка справедлива только для упругих систем. , где
, где 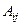 – работа сил i - го состояния на перемещение точек их положения, вызванных силами j – го состояния,
– работа сил i - го состояния на перемещение точек их положения, вызванных силами j – го состояния, 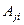 – наоборот. Согласно этой теореме
– наоборот. Согласно этой теореме  и потому
и потому 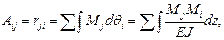
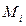 - моменты от единичных смещений.
- моменты от единичных смещений.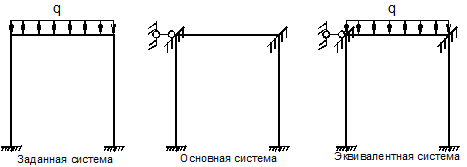
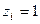 . Тогда на основании рис. 28
. Тогда на основании рис. 28  , то из (14.30) следует, что
, то из (14.30) следует, что 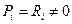 , т.е.
, т.е.  будут представлять собой опорные реакции от внешней нагрузки внутри пролётов. Система будет эквивалентна заданной, если дополнительные связи будут упругими и допускать действительные перемещения, имеющие место в данной системе. Этого можно добиться, если приравнять к нулю реакции всех введённых дополнительных связей, которые препятствуют поворотам и линейным смещениям
будут представлять собой опорные реакции от внешней нагрузки внутри пролётов. Система будет эквивалентна заданной, если дополнительные связи будут упругими и допускать действительные перемещения, имеющие место в данной системе. Этого можно добиться, если приравнять к нулю реакции всех введённых дополнительных связей, которые препятствуют поворотам и линейным смещениям  Эту мысль и выражают собой канонические уравнения (14.30).
Эту мысль и выражают собой канонические уравнения (14.30).
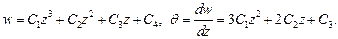
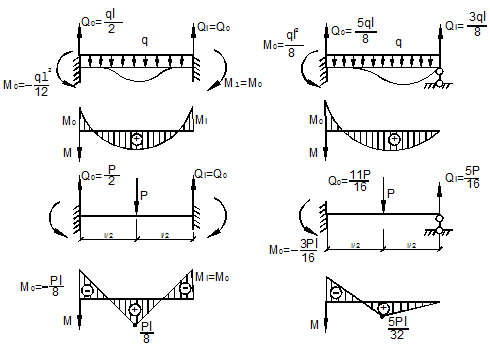
 прогиб
прогиб 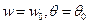 , а при
, а при 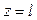 прогиб
прогиб 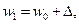
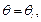 поэтому
поэтому


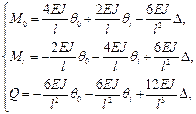 (14.31)
(14.31)
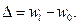
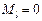 , что, согласно (14.31), позволяет найти:
, что, согласно (14.31), позволяет найти: (14.32)
(14.32)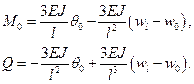
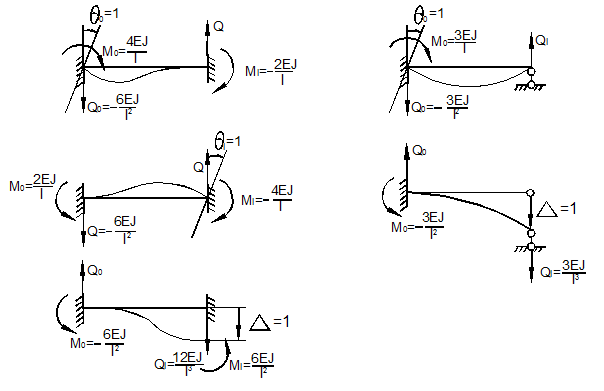
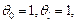
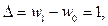 согласно (14.31), (14.32). Зная реакции в опорах от единичных перемещений, можно найти коэффициенты
согласно (14.31), (14.32). Зная реакции в опорах от единичных перемещений, можно найти коэффициенты 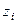 . Зная последние по формулам
. Зная последние по формулам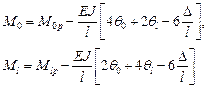
 (14.33)
(14.33)


