Использование свойств симметрии при раскрытии статической неопределимости
Использование метода сил для расчета систем с высокой степенью статической неопределимости связано с решением совместной системы большого количества линейных уравнений. Даже самый экономичных метод решения таких систем – алгоритм Гаусса – требует Основным средством для достижения этой цели является использование симметрии. Стержневая система является симметричной, если симметричны не только оси и опорные закрепления (геометрическая симметрия), но и жесткости (упругая симметрия). При этом внешняя нагрузка может быть и несимметричной. При выборе основной системы лишние неизвестные следует выбирать в виде симметричных и обратно симметричных усилий. Симметричные неизвестные создают симметричные эпюры моментов, а обратно симметричные неизвестные – кососимметричные эпюры. Такие эпюры обладают свойством взаимной ортогональности, т.е. результат их перемножения равен нулю:
Ортогонализация эпюр может достигаться различными способами: 1) выбор симметричной основной системы; 2) выбор симметричных и обратносимметричных неизвестных; 3) группировка неизвестных; 4) устройство жестких консолей (способ упругого центра); 5) использование статически неопределимой основной системы; 6) разложение произвольной нагрузки на симметричную и обратносимметричную составляющие. Рассмотрим раму, имеющую ось геометрической симметрии (рис.19, а). Заменим внешнюю нагрузку ей статически эквивалентной, такой, что она представляет сумму симметричной (рис.19, б) и кососимметричной (рис.19, в) нагрузок относительно оси геометрической симметрии.
а) б) в) Рис. 19
Аналогично можно классифицировать внутренние силовые факторы в произвольном сечении стержневой системы (рис.20). Изгибающие моменты М Х, М У, нормальная сила N являются зеркальным отражением друг друга относительно плоскости поперечного сечения. Эти внутренние силовые факторы назовём симметричными. Остальные (перерезывающие силы Q x, Q y и крутящий момент М z) назовём антисимметричными или кососимметричными силовыми факторами.
Рис. 20 Докажем теперь положение: у геометрически симметричной рамы в плоскости симметрии при симметричной внешней нагрузке обращаются в нуль кососимметричные внутренние силовые факторы, а при кососимметричной внешней нагрузке – симметричные силовые факторы (рис.21). Канонические уравнения метода сил для изображённой на рис.19 трижды статически неопределимой рамы имеют вид
а) б) Рис. 21
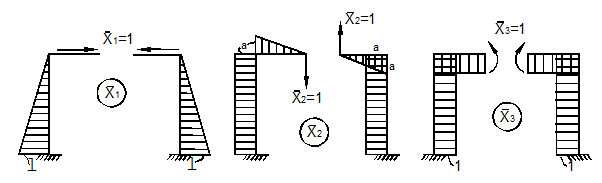
На рис. 22 приведены эпюры изгибающих моментов от единичных сил. На основании этих эпюр находим:
а) б) в) Рис. 22
Следовательно, канонические уравнения (14.19) принимают вид
На рис. 23 приведены эпюры моментов от внешних симметричной (рис.23, а) и кососимметричной (рис.23, б) нагрузок. В первом случае симметричной внешней нагрузки имеем:
а) б) Рис. 23
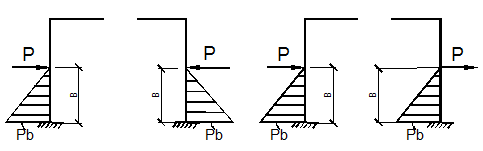
Из (14.20) следует Х 2 = 0, т.е. при симметричной внешней нагрузке обращается в нуль кососимметричный силовой фактор (перерезывающая сила), что и требовалось доказать. Во втором случае кососимметричной внешней нагрузки имеем:
Канонические уравнения (14.20) принимают вид
Т.к. определитель системы двух первых уравнений (14.21)
то Полученные результаты могут быть распространены на пространственные стержневые системы.
|

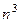 вычислительных операций (где n – число уравнений, т.е. степень статической неопределимости системы), при условии, что все коэффициенты системы отличны от нуля. В связи с этим нужно стремиться так выбрать основную систему, чтобы возможно большее число побочных единичных перемещений
вычислительных операций (где n – число уравнений, т.е. степень статической неопределимости системы), при условии, что все коэффициенты системы отличны от нуля. В связи с этим нужно стремиться так выбрать основную систему, чтобы возможно большее число побочных единичных перемещений  ,
,  и свободных членов
и свободных членов  обратилось в ноль.
обратилось в ноль. (14.18)
(14.18)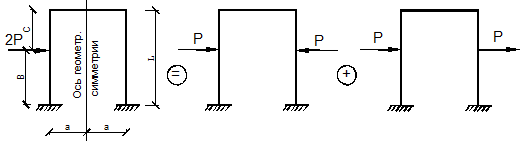
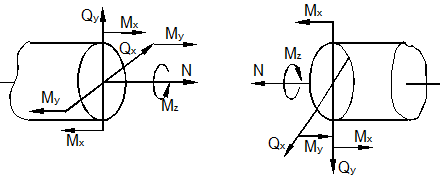

 (14.19)
(14.19)
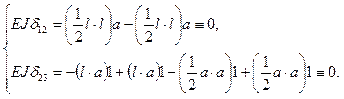
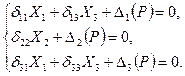 (14.20)
(14.20)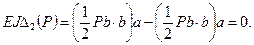
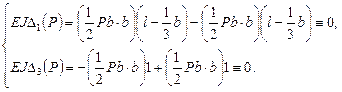
 (14.21)
(14.21)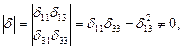
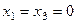 , что и требовалось доказать.
, что и требовалось доказать.


