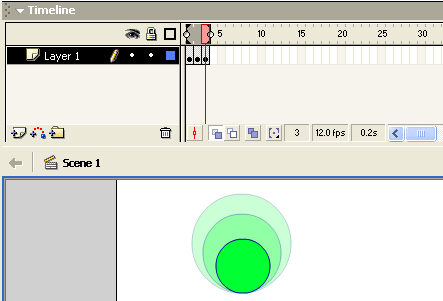
Рис.3. Калькирование
Калькирование позволяет одновременно просматривать несколько кадров (рис.3). При щелчке на одной из трех кнопок калькирования на временной шкале появляются маркеры калькирования, расположенные вокруг текущего кадра. Эти маркеры указывают на тот диапазон кадров, которые отображаются при включении калькирования. Для изменения положения любого из этих маркеров вручную, щелкните на нем и перетащите его в нужное положение на временной шкале. Для управления способом отображения калькируемых кадров также можно воспользоваться раскрывающимся меню Modify Onion Markers (Изменить маркеры калькирования). По умолчанию текущий кадр отображается в полном цвете, а остальные кадры отображаются полупрозрачно. Как показано на рис, они отображаются так, как если бы были нарисованы на кальке, а затем наложены друг на друга (Обратите внимание, как меняется прозрачность объектов по мере удаления от текущего кадра. Это важная визуальная подсказка, которая работает как в режиме обычного калькирования, так и в режиме контурного калькирования.) Редактировать можно только выделенный кадр, но это свойство полезно еще и потому, что позволяет видеть, как редактирование влияет на воспроизведение всего выделенного фрагмента анимации. Свойство калькирования играет важную роль при редактировании покадровой анимации, потому что позволяет одновременно отображать каждый кадр анимационного фрагмента, не переключаясь между кадрами





