Suppose 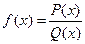 is a rational function; that is,
is a rational function; that is, 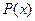 and
and 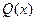 are polynomial functions. If the degree of
are polynomial functions. If the degree of 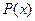 is greater than or equal to the degree of
is greater than or equal to the degree of 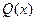 , then by long division,
, then by long division, 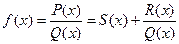 where
where  is a proper rational fraction; that is, the degree of
is a proper rational fraction; that is, the degree of  is less than the degree of
is less than the degree of 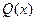 . A theorem in advanced algebra states that every proper rational function can be expressed as a sum
. A theorem in advanced algebra states that every proper rational function can be expressed as a sum

where 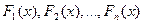 are rational functions of the form
are rational functions of the form
 or
or 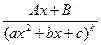
in which the denominators are factors of 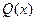 . The sum is called the partial fraction decomposition of
. The sum is called the partial fraction decomposition of  . The first step is finding the form of the partial fraction decomposition of
. The first step is finding the form of the partial fraction decomposition of  is to factor
is to factor 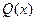 completely into linear and irreducible quadratic factors, and then collect all repeated factors so that
completely into linear and irreducible quadratic factors, and then collect all repeated factors so that 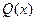 is expressed as a product of distinct factors of the form
is expressed as a product of distinct factors of the form
 and
and 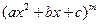 .
.
From these factors we can determine the form of the partial fraction decomposition using the following two rules:
Linear Factor Rule:For each factor of the form  , the partial fraction decomposition contains the following sum of m partial fractions:
, the partial fraction decomposition contains the following sum of m partial fractions:
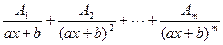
where A 1, A 2,..., Am are constants to be determined.
Quadratic Factor Rule:For each factor of the form 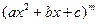 , the partial fraction decomposition contains the following sum of m partial fractions:
, the partial fraction decomposition contains the following sum of m partial fractions:

where A 1, A 2,..., Am, B 1, B 2, …, Bm are constants to be determined.

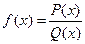 is a rational function; that is,
is a rational function; that is, 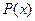 and
and 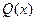 are polynomial functions. If the degree of
are polynomial functions. If the degree of 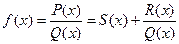 where
where  is a proper rational fraction; that is, the degree of
is a proper rational fraction; that is, the degree of  is less than the degree of
is less than the degree of 
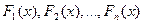 are rational functions of the form
are rational functions of the form or
or 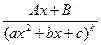
 and
and 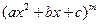 .
.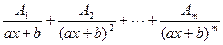
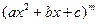 , the partial fraction decomposition contains the following sum of m partial fractions:
, the partial fraction decomposition contains the following sum of m partial fractions:



