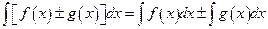When solving a differential equation of the form 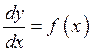 , we solve for
, we solve for  , giving us the equivalent differential form
, giving us the equivalent differential form  . The operation of finding all solutions of this equation is called antidifferentiation or indefinite integration and is denoted by an integral sign
. The operation of finding all solutions of this equation is called antidifferentiation or indefinite integration and is denoted by an integral sign 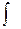 . The general solution is denoted by
. The general solution is denoted by 
Definition. Suppose f is a function defined on an interval I and suppose further that f has an antiderivative on the interval I. The family of all antiderivatives of f is called the indefinite integral of f and is denoted by the symbol 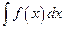 (read the integral of f with respect to x). In this notation the function is called the integrand of the indefinite integral. The process of finding the indefinite integral is called integration or, sometimes anti-differentiation. More specifically, given a function f, the expression “integrating f ” means “finding the indefinite integral of f ”.
(read the integral of f with respect to x). In this notation the function is called the integrand of the indefinite integral. The process of finding the indefinite integral is called integration or, sometimes anti-differentiation. More specifically, given a function f, the expression “integrating f ” means “finding the indefinite integral of f ”.
There is a difference between an antiderivative and the indefinite integral. An antiderivative is a member of the family of functions represented by the indefinite integral. In the above example, 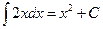 , where C is a constant. The functions
, where C is a constant. The functions 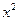 ,
,  and
and  are all members of the family
are all members of the family 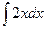 and are all antiderivatives of the function
and are all antiderivatives of the function 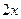 . It is also correct to write
. It is also correct to write 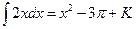 , where K is a constant. The difference is the choice of constants, where in this case
, where K is a constant. The difference is the choice of constants, where in this case 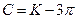 .
.
Notice that all these curves are “parallel” in the sense that they never cross each other since they are translates of the function 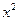 . To get a particular antiderivative one needs to know a specific point the antiderivative passes through. For example, if we want the curve that is a member of the family
. To get a particular antiderivative one needs to know a specific point the antiderivative passes through. For example, if we want the curve that is a member of the family 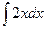 that passes through the point
that passes through the point 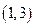 , we have
, we have  and
and 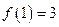 . So
. So 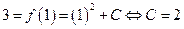 and it follows that
and it follows that 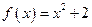 .
.
The process of integration involves finding one antiderivative of the given function so that the indefinite integral is that one antiderivative plus the constant of integration. This can be easy for certain functions because we know the differentiation formulae. For example, because 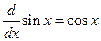 , it follows that
, it follows that  , C a constant. Here are the integration formulae that follow directly from the appropriate differentiation formulae: The symbol C is a constant (called the constant of integration). For any differentiable function
, C a constant. Here are the integration formulae that follow directly from the appropriate differentiation formulae: The symbol C is a constant (called the constant of integration). For any differentiable function  it is always the case that
it is always the case that 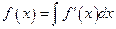 meaning that the function
meaning that the function  is a member of the family
is a member of the family 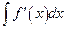 .
.
1. 
2.  for any constant
for any constant  . Notice that when
. Notice that when 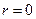 , the
, the
formula reduces to  or just
or just 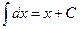 .
.
3. 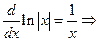

4. 

5. 
6. 
7. 
8. 
9. 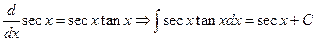
10. 
In fact every differentiation formula provides an integration formula. Consider the differentiation formula 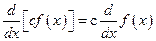 . This is a statement that two derivatives are equal. So the families of antiderivatives are also the same families. Therefore
. This is a statement that two derivatives are equal. So the families of antiderivatives are also the same families. Therefore 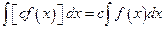 . In the same manner,
. In the same manner,
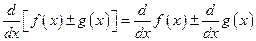
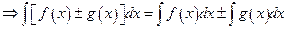 .
.
For reference, number these formulae as
11. 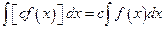
12. 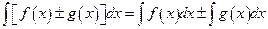
These two formulae and those above can be combined to produce integrals of more complicated functions as shown in the examples below.

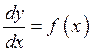 , we solve for
, we solve for  , giving us the equivalent differential form
, giving us the equivalent differential form  . The operation of finding all solutions of this equation is called antidifferentiation or indefinite integration and is denoted by an integral sign
. The operation of finding all solutions of this equation is called antidifferentiation or indefinite integration and is denoted by an integral sign 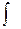 . The general solution is denoted by
. The general solution is denoted by 
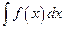 (read the integral of f with respect to x). In this notation the function is called the integrand of the indefinite integral. The process of finding the indefinite integral is called integration or, sometimes anti-differentiation. More specifically, given a function f, the expression “integrating f ” means “finding the indefinite integral of f ”.
(read the integral of f with respect to x). In this notation the function is called the integrand of the indefinite integral. The process of finding the indefinite integral is called integration or, sometimes anti-differentiation. More specifically, given a function f, the expression “integrating f ” means “finding the indefinite integral of f ”.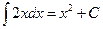 , where C is a constant. The functions
, where C is a constant. The functions 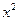 ,
,  and
and  are all members of the family
are all members of the family 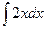 and are all antiderivatives of the function
and are all antiderivatives of the function 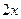 . It is also correct to write
. It is also correct to write 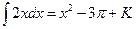 , where K is a constant. The difference is the choice of constants, where in this case
, where K is a constant. The difference is the choice of constants, where in this case 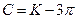 .
.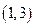 , we have
, we have  and
and 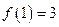 . So
. So 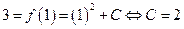 and it follows that
and it follows that 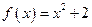 .
.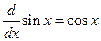 , it follows that
, it follows that  , C a constant. Here are the integration formulae that follow directly from the appropriate differentiation formulae: The symbol C is a constant (called the constant of integration). For any differentiable function
, C a constant. Here are the integration formulae that follow directly from the appropriate differentiation formulae: The symbol C is a constant (called the constant of integration). For any differentiable function  it is always the case that
it is always the case that 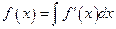 meaning that the function
meaning that the function 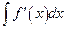 .
.
 for any constant
for any constant  . Notice that when
. Notice that when 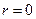 , the
, the or just
or just 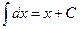 .
.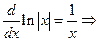







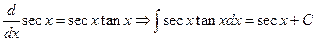

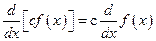 . This is a statement that two derivatives are equal. So the families of antiderivatives are also the same families. Therefore
. This is a statement that two derivatives are equal. So the families of antiderivatives are also the same families. Therefore 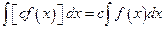 . In the same manner,
. In the same manner,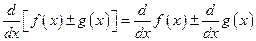
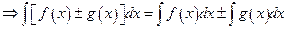 .
.