Let  be a function differentiable on an interval J. The function f is called convex (concave) on J, if all points of its graph on J lie above (below) any tangent line to
be a function differentiable on an interval J. The function f is called convex (concave) on J, if all points of its graph on J lie above (below) any tangent line to 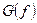 on this interval (excepting point of tangency). Let f be continuous at a point
on this interval (excepting point of tangency). Let f be continuous at a point 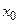 . If there exists
. If there exists  such that f is concave (convex) in
such that f is concave (convex) in  and convex (concave) in
and convex (concave) in 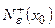 , the point
, the point 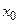 is called the point of inflection of
is called the point of inflection of  .
.
The second Derivative Test for Concavity and Convexity:
If 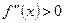 , for each
, for each 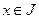 , then
, then  is convex on J,
is convex on J,
if  , for each
, for each 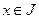 , then
, then  is concave on J.
is concave on J.
It follows:
If  is continuous at
is continuous at 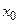 and
and 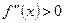 (
( ) in
) in  and
and  (
(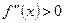 ) in
) in 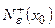 , then
, then 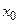 is a point of inflection.
is a point of inflection.
Moreover: If 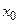 is a point of inflection of f, then either
is a point of inflection of f, then either  or
or 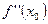 doesn’t exist.
doesn’t exist.
If f is three times differentiable at a point 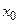 ,
,  and
and 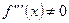 , then
, then 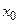 is a point of inflection.
is a point of inflection.
Definition 6. Given that  is continuous on
is continuous on 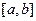 , if any
, if any  such that
such that
 (i)
(i)  (ii)
(ii) 
 Concave Downward Concave Upward
Concave Downward Concave Upward
Theorem 3. If  is a function on
is a function on 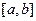 such that
such that  is second differentiable on
is second differentiable on 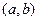 then
then
(i) 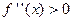 iff
iff  is concave upward on
is concave upward on 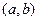
(ii)  iff
iff  is concave downward on
is concave downward on 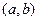 .
.
Definition 7. Let 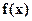 be a continuous function. A point
be a continuous function. A point  on the graph of
on the graph of  is a point of inflexion (point of inflection) if the graph on one side of this point is concave downward and concave upward on the other side. That is, the graph changes concavity at
is a point of inflexion (point of inflection) if the graph on one side of this point is concave downward and concave upward on the other side. That is, the graph changes concavity at 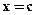 .
.

Note A point of inflexion of a curve 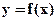 must be a continuous point but need not be differentiable there. In Figure (c), R is a point of inflexion of the curve but the function is not differentiable at
must be a continuous point but need not be differentiable there. In Figure (c), R is a point of inflexion of the curve but the function is not differentiable at 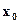 .
.
Theorem 4. If 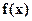 is second differentiable function and attains a point of inflexion at
is second differentiable function and attains a point of inflexion at 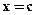 , then
, then
 .
.
Note:
(i) max. or min. point but not derivative.
(ii) point of inflexion may not be obtained by solving  where
where 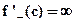 and
and 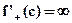 such that
such that 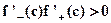 .
.
(iii) Let 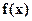 be a function which is second differentiable in a neighborhood of a point of inflexion iff
be a function which is second differentiable in a neighborhood of a point of inflexion iff 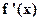 does not change sign as
does not change sign as 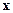 increases through (sign gradient test)
increases through (sign gradient test)
– if  and
and  , then
, then 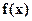 attains a relative max. or relative min.
attains a relative max. or relative min.
– if  and
and  , then
, then 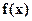 attains an inflexion point at
attains an inflexion point at  .
.

 be a function differentiable on an interval J. The function f is called convex (concave) on J, if all points of its graph on J lie above (below) any tangent line to
be a function differentiable on an interval J. The function f is called convex (concave) on J, if all points of its graph on J lie above (below) any tangent line to 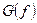 on this interval (excepting point of tangency). Let f be continuous at a point
on this interval (excepting point of tangency). Let f be continuous at a point 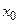 . If there exists
. If there exists  such that f is concave (convex) in
such that f is concave (convex) in  and convex (concave) in
and convex (concave) in 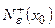 , the point
, the point 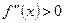 , for each
, for each 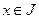 , then
, then  , for each
, for each  or
or 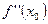 doesn’t exist.
doesn’t exist.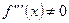 , then
, then  is continuous on
is continuous on 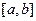 , if any
, if any  such that
such that (i)
(i)  (ii)
(ii) 
 Concave Downward Concave Upward
Concave Downward Concave Upward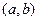 then
then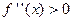 iff
iff  iff
iff 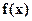 be a continuous function. A point
be a continuous function. A point  on the graph of
on the graph of  is a point of inflexion (point of inflection) if the graph on one side of this point is concave downward and concave upward on the other side. That is, the graph changes concavity at
is a point of inflexion (point of inflection) if the graph on one side of this point is concave downward and concave upward on the other side. That is, the graph changes concavity at 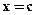 .
.
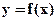 must be a continuous point but need not be differentiable there. In Figure (c), R is a point of inflexion of the curve but the function is not differentiable at
must be a continuous point but need not be differentiable there. In Figure (c), R is a point of inflexion of the curve but the function is not differentiable at 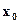 .
. .
. where
where 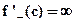 and
and 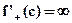 such that
such that 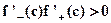 .
.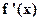 does not change sign as
does not change sign as 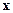 increases through (sign gradient test)
increases through (sign gradient test) and
and  , then
, then  , then
, then  .
.


