Differential of Function
Suppose that there is the differentiable function y=f(x) on the interval [ a; b ].It follows that
Acodrding to the principal theorem on limits, we have
Find the increment
Definition. The principal part of the increment of function (*) is called a differential of function and is denoted by
Find the differential of function у=х by definition
i.e., the differential of the independent variable equals the increment of this variable. Substituting increment Dх by dх in the ratio, we obtain
The differential of function equals the derivative of this function, multiplied by the differential of argument. For example, y = cos2 x, dy = –2 cos x ·sin x·dx. As the differential is the derivative multiplied by the differential of argument, then the differential of function has absolutely all properties, which the derivatives have, i.e., d (u ± v) = du ± dv, d (u·v) = vdu+udv,
|

 .
.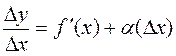 ,
,  ®0 as D х ®0.
®0 as D х ®0. . (*)
. (*)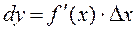 .
.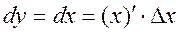 or
or 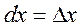 ,
,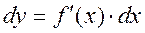 . (8)
. (8)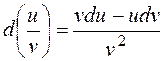 .
.


