Theorem 1. Let 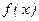 be continuous on [a, b] and differentiable on (a, b).
be continuous on [a, b] and differentiable on (a, b). 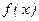 is a constant
is a constant
function if and only if 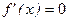 for all
for all  .
.
Definition 1. A function 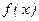 is said to be monotonic increasing (resp. monotonic decreasing)
is said to be monotonic increasing (resp. monotonic decreasing)
or simply increasing (resp. decreasing) on an interval  if and only if
if and only if  , if
, if 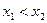
then 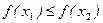 (resp.
(resp.  , if
, if 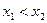 , then
, then 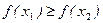 ).
).
Definition 2. A function 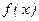 is said to be strictly increasing (resp. strictly decreasing) on an
is said to be strictly increasing (resp. strictly decreasing) on an
interval  if and only if
if and only if  , if
, if 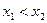 then
then 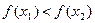 (resp.
(resp.  , if
, if 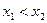 ,
,
then 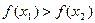 ).
).
Theorem 2. Let 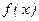 be continuous on [a, b] and differentiable on (a, b). Then
be continuous on [a, b] and differentiable on (a, b). Then
(a) if 

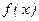 is strictlyincreasing on [a, b]; and
is strictlyincreasing on [a, b]; and
(b)if 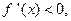

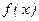 is strictly decreasing on [a, b].
is strictly decreasing on [a, b].
Definition 3. A neighborhood of a point  is an open interval containing
is an open interval containing  , i.e.
, i.e.  is a neighborhood of
is a neighborhood of  for some
for some  .
.
Definition 4. A function 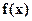 is said to attain a relative maximum (minimum) at a point
is said to attain a relative maximum (minimum) at a point  if
if
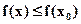 (
(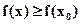 ) in a certain neighborhood of
) in a certain neighborhood of  , i.e.
, i.e.  such that
such that 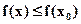 (
(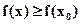 ) for
) for 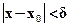 .
.

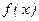 be continuous on [a, b] and differentiable on (a, b).
be continuous on [a, b] and differentiable on (a, b). 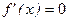 for all
for all  .
. if and only if
if and only if  , if
, if 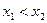
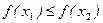 (resp.
(resp. 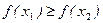 ).
).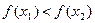 (resp.
(resp. 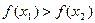 ).
).

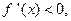
 is an open interval containing
is an open interval containing  is a neighborhood of
is a neighborhood of  .
.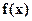 is said to attain a relative maximum (minimum) at a point
is said to attain a relative maximum (minimum) at a point 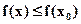 (
(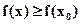 ) in a certain neighborhood of
) in a certain neighborhood of  such that
such that 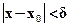 .
.


