If a function f gets close to a certain number L when x gets larger and larger, then we say that the limit as x goes to infinity is L and we write:  . Likewise, if f gets close to L when x gets smaller and smaller, then the limit as x goes to negative infinity is L and we write:
. Likewise, if f gets close to L when x gets smaller and smaller, then the limit as x goes to negative infinity is L and we write:  . In both cases, the line y = L is a horizontal asymptote of f.
. In both cases, the line y = L is a horizontal asymptote of f.
 Example:
Example: 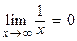 because when x is very large,
because when x is very large,  is close to 0. The x -axis is a horizontal asymptote of the function
is close to 0. The x -axis is a horizontal asymptote of the function 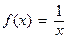 :
:
If a function 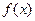 gets larger and larger as x gets close to a number a, then it “goes to infinity” and we write:
gets larger and larger as x gets close to a number a, then it “goes to infinity” and we write: 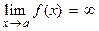 . The line x = a is a vertical asymptote of f. Similarly, if
. The line x = a is a vertical asymptote of f. Similarly, if 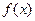 gets smaller and smaller as x gets close to a, then it “goes to negative infinity” and we write:
gets smaller and smaller as x gets close to a, then it “goes to negative infinity” and we write:  . Again, the line x = a is a vertical asymptote of f.
. Again, the line x = a is a vertical asymptote of f.
An important result:
If 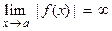 then
then 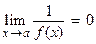 . This is because one over a very large positive number and one over a huge negative number are both close to 0.
. This is because one over a very large positive number and one over a huge negative number are both close to 0.
Inclined asymptotes have an equation y = kx + q and their position is arbitrary except vertical. In order a straight line y = kx + q be an asymptote, the coefficients k and q must satisfy at least one pair of the following conditions
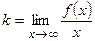 and
and  (k and b are numbers).
(k and b are numbers).
Naturally these limits must be finite real numbers. A certain function can have maximally two inclined asymptotes.

 . Likewise, if f gets close to L when x gets smaller and smaller, then the limit as x goes to negative infinity is L and we write:
. Likewise, if f gets close to L when x gets smaller and smaller, then the limit as x goes to negative infinity is L and we write:  . In both cases, the line y = L is a horizontal asymptote of f.
. In both cases, the line y = L is a horizontal asymptote of f. Example:
Example: 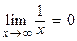 because when x is very large,
because when x is very large,  is close to 0. The x -axis is a horizontal asymptote of the function
is close to 0. The x -axis is a horizontal asymptote of the function 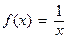 :
: gets larger and larger as x gets close to a number a, then it “goes to infinity” and we write:
gets larger and larger as x gets close to a number a, then it “goes to infinity” and we write: 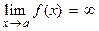 . The line x = a is a vertical asymptote of f. Similarly, if
. The line x = a is a vertical asymptote of f. Similarly, if  . Again, the line x = a is a vertical asymptote of f.
. Again, the line x = a is a vertical asymptote of f.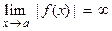 then
then 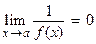 . This is because one over a very large positive number and one over a huge negative number are both close to 0.
. This is because one over a very large positive number and one over a huge negative number are both close to 0.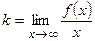 and
and  (k and b are numbers).
(k and b are numbers).


