Properties of differentiable functions
Fermat's Theorem. Let Rolle's Theorem. If a function (1) (2) (3) then there exists at least a point Lagrange's Theorem.
(1) continuous on the closed interval (2) differentiable in the open interval then there exists at least a point
Limits- indeterminate forms and L’Hospital’s Rule I. Indeterminate Form of the Type We have previously studied limits with the indeterminate form
However, there is a general, systematic method for determining limits with the indeterminate form
L’Hospital’s Rule.
The Bernoulli-L'Hopital Rule This rule is used for finding the ratio limits of the form Theorem 1. Suppose that there are differentiable functions f(x) and j(x) on the interval [a;b] and f(a)=j(a)=0, then having limit
In the following examples, we will use the following three-step process:
Step 1. Check that the limit of Step 2. Differentiate f and g separately. [ Note: Do not differentiate Step 3. Find the limit of
Example 6:
II. Indeterminate Form of the Type We have previously studied limits with the indeterminate form
Example 7:
However, we could use another version of L’Hospital’s Rule.
L’Hospital’s Rule for Form Suppose that f and g are differentiable functions on an open interval containing x = a, except possibly at x = a, and that
in the case of a limit as
III. Indeterminate Form of the Type
Indeterminate forms of the type forms of type Example 8: IV. Indeterminate Form of the Type
A limit problem that leads to one of the expressions
is called an indeterminate form of type
are not indeterminate, since the two terms work together (the first two produce a limit of Example 9:
V. Indeterminate Forms of the Types Limits of the form (1) (2) (3)
The limit on the righthand side of the equation will usually be an indeterminate limit of the type (4) Finally, Example 10: Find
This is an indeterminate form of the type Thus,
Taylor’s formula
Suppose we’re working with a function f(x) that is continuous and has n+1 continuous derivatives on an interval about x = 0. We can approximate f near 0 by a polynomial • For n = 0, the best constant approximation near 0 is • For n = 1, the best linear approximation near 0 is • For n = 2, the best quadratic approximation near 0 is Continuing this process,
This is the Taylor polynomial of degree n about 0 (also called the Maclaurin series of degree n). More generally, if f has n+1 continuous derivatives at x = a, the Taylor series of degree n about a is
This formula approximates f (x) near a. Taylor’s Theorem gives bounds for the error in this approximation: Taylor’s Theorem: Suppose f has n+1 continuous derivatives on an open interval containing a. Then for each x in the interval,
where the error term This form for the error
if and only if
|

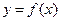 be defined and differentiable on an open interval (a, b). If
be defined and differentiable on an open interval (a, b). If  attains its absolute maximum or absolute minimum (both are called absolute extremum) at
attains its absolute maximum or absolute minimum (both are called absolute extremum) at 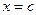 , where
, where 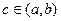 , then
, then 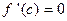 .
.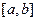 ,
,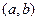 ,
, ;
; such that
such that 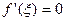 .
. If a function
If a function 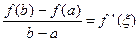 .
.


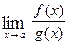 is an indeterminate form of the type
is an indeterminate form of the type 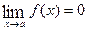 and
and 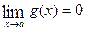 . Since f and g are differentiable functions at x = a, then f and g are continuous at x = a; that is,
. Since f and g are differentiable functions at x = a, then f and g are continuous at x = a; that is, 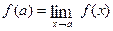 = 0 and
= 0 and  = 0. Furthermore, since f and g are differentiable functions at x = a, then
= 0. Furthermore, since f and g are differentiable functions at x = a, then 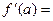
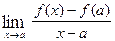 and
and  . Thus, if
. Thus, if 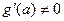 , then
, then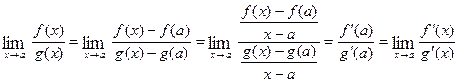 if
if 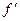 and
and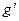 are continuous at x = a. This illustrates a special case of the technique known as
are continuous at x = a. This illustrates a special case of the technique known as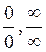
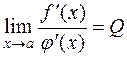 , there is the limit which equals
, there is the limit which equals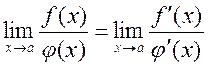 .
.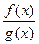 is an indeterminate form of type
is an indeterminate form of type 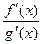 . If this limit is finite,
. If this limit is finite, 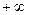 , or
, or 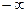 , then it is equal to the limit of
, then it is equal to the limit of 
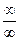

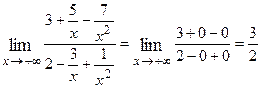
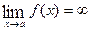 and
and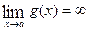 . If
. If 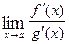 has a finite limit, or if this limit is
has a finite limit, or if this limit is 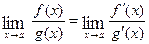 . Moreover, this statement is also true
. Moreover, this statement is also true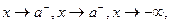 or as
or as 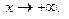

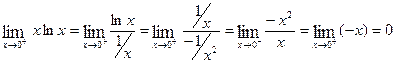
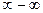
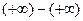 ,
,  ,
,  ,
, 
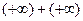 ,
,  ,
,  ,
, 
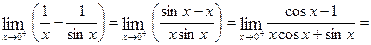
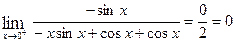
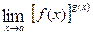
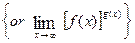 frequently give rise to indeterminate forms of the types
frequently give rise to indeterminate forms of the types 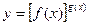
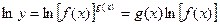
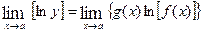
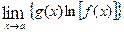 = L.
= L.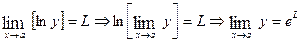 .
. .
. . Let
. Let 
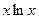 .
. 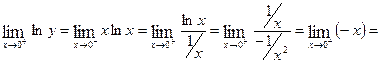 0.
0.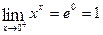 .
. of degree n:
of degree n: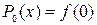 which matches f at 0.
which matches f at 0.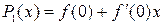 . Note that
. Note that 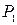 matches f at 0 and
matches f at 0 and 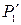 matches
matches 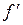 at 0.
at 0.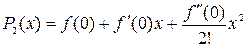 . Note that
. Note that 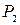 ,
, 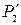 , and
, and 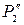 match
match 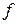 ,
, 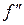 , respectively, at 0.
, respectively, at 0.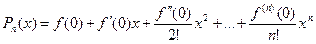 .
.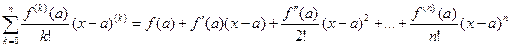 .
.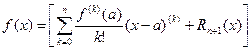 ,
, satisfies
satisfies 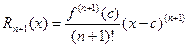 for some c between a and x.
for some c between a and x. ,
,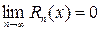 .
.