Method of Logarithmic Differentiation
The conception of this method is the following: beforehand, we obtain the logarithm of the assigned function, and only then differentiate the result. In applications more often we encounter with two cases with the logarithmic differentiation. 1. Find the derivative of the product of several functions y=u1(х.)· u2.(х)· u3.(х)· …·un(х). Let us obtain the logarithm of both parts, using the property of the logarithm of product ln y = ln u1.+ ln u2 + ln u3 +…+ ln un. Differentiate both parts, the left one - as the implicit function
Multiplying both parts by у and substituting it by the function itself, we obtain
Example 1. Find the variable
Find the logarithm of both parts
Differentiate both parts
Then, we obtain the required derivative
Then out of this, we obtain the required derivative
2. Consider the function y=u (x) v (x), here the base u (x) and v (x) the power are functions; thus, the function is called a power-exponential function. Obtain the derivative of this function. By the analogy with the first case, obtain the logarithm and use the property of the logarithm of power ln y = v(x). ln u(x). Differentiate both parts
multiplying both parts by у and substituting by the power-exponential function; thus, we obtain the derivative
Example 2. Find the derivative y=xx , ln y = x. ln x,
Thus, the required derivtive is
|
.
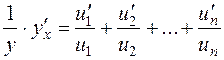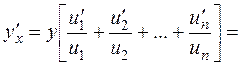u1(х). u2.(х) ….un(х) 
.
.
.
.
.
,
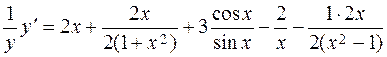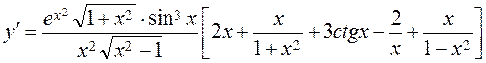. (7)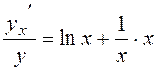
.
.
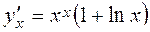