INTEGRAL CALCULUS
Problem 1. Find indefinite integrals
Problem 2. Calculate definite integrals
Problem 3. 1. Find the area bounded by the curve 2. Find the area of the ellipse 3. Find the area bounded by the curve 4. Find the area of the lemniscate 5. Find the length of the cissoid 6. Find the area bounded by the parabola 7. Find the area bounded by the ellipse 8. Find the area of the ellipse whose parametric equations are 9. Find the parabola 10. Find the area bounded by the parabola 11. Find the bounded area between the curves 12. Find the area of an arch of the cycloid 13. Find the area of the cardioid 14. Find the area of one loop of the curve 15. Find the area between the curve 16. Sketch the graph 17. Sketch the graph 18. Find the area in the first quadrant between the graph of 19. Find the circumference of a circle of radius R. 20. Find the entire length of the hypocycloid 21. Find the volume of the solid generated by revolving about the x-axis the area bounded by the curve 22. Find the volume of the solid generated by revolving about the line y=8 the area bounded by the curve 23. The area bounded by the curve xy=1 and the lines x=1, x=3 and y=0 is evolved about the x-axis. Find the volume generated. 24. The smaller segment cut from the circle 25. Find the volume generated by revolving about the line y=x the area bounded by the line 26. The area bounded by the hyperbola 27. Find the volume generated by revolving about the line x=2, the area bounded by the parabola 28. Find the area of the surface generated by revolving the curve 29. Find the area of the surface generated by revolving the curve 30. Find the area of the surface generated by revolving an arch of the cycloid
REFERENCES:
1. Atkinson, K.E. (1993), Elementary Numerical Analysis, 2nd ed., John Wiley (New York). 2. Blachman, N. (1999), Mathematica: a Practical Approach, 2nd ed., Prentice Hall (Upper Saddle River, N.J). 3. Bracewell, R.N. (1986), The Fourier Transform and Its Applications, 2nd ed., McGraw-Hill (New York). 4. Edwards, C.H., Penney, D.E. (1998), Calculus with Analytic Geometry, 5th ed., Prentice Hall (Upper Saddle River, N.J). 5. Efimov N.V. «A short course of analytical geometry». M. 1967. 6. Franklin, J.N. (1968), Matrix Theory, Prentice-Hall (Englewood Cliffs, NJ). 7. Gerald, C.F. (1999), Applied Numerical Analysis, 6th ed., Addison-Wesley (Cambridge, MA). 8. Golub, G.H. (1996), Matrix Computations, 3rd ed., Johns Hopkins University Press (Baltimore). 9. Greenberg, M.D. (1998), Advanced Engineering Mathematics, 2nd ed., Prentice Hall (Upper Saddle River, N.J). 10. Gusak A.A. (1983, 1984), «Higher Mathematics. Tutorial», Minsk. Vol.1, 2. 11. Gusak A.A. (1988), «Problems and exercises in higher mathematics», Minsk.V 1, 2. 12. Hildebrand, F.B. (1974), Introduction to Numerical Analysis, 2nd ed., McGraw-Hill (New York). 13. Hildebrand, F.B. (1976), Advanced Calculus for Applications, 2nd ed., Prentice-Hall (Englewood Cliffs, NJ). 14. Kreyszig, E. (1999), Advanced Engineering Mathematics, 8th ed., John Wiley (New York). 15. Minorsky V.P. (1987), «Problems in higher mathematics». M. Science. 16. Olver, F.W.J. (1974), Asymptotics and Special Functions, Academic Press (New York). 17. O'Neil, P.V. (1995), Advanced Engineering Mathematics, 4th ed., PWS-Kent Pub. (Boston). 18. Piskunov N.S. (1985), «The differential and integral calculus». M. Vol 1, 2. 19. Privalov N. N. (1964), «Analytic geometry», M. 20. Spiegel, M.R. (ed.) (1968), Mathematical Handbook of Formulas and Tables, McGraw-Hill (New York). 21. Shipachev V.S. (2001), «Higher Mathematics», M. 22. Stoer, J., Bulirsch, R. (1993), Introduction to Numerical Analysis, 2nd ed., Springer-Verlag (New York). 23. Strang, G. (1988), Linear Algebra and Its Applications, 3rd ed., Harcourt, Brace, Jovanovich (San Diego). 24. Strang, G. (1991), Calculus, Wellesley-Cambridge Press (Wellesley, MA). 25. Strang, G. (1998), Introduction to Linear Algebra, Wellesley-Cambridge Press (Wellesley, MA). 26. Wang, Z.X. (1989), Special Functions, World Scientific (Singapore). 27. Watson, G.N. (1944), A Treatise on the Theory of Bessel Functions, 2nd ed., Macmillan (New York). 28. Wolfram, S. (1999), The Mathematica Book, 4th ed., Cambridge Univ. Press (New York). 29. Wylie, C.R. (1995), Advanced Engineering Mathematics, 6th ed., McGraw-Hill (New York). 30. Zwillinger, D. (ed.) (1996), CRC Standard Mathematical Tables and Formulae, 30th ed., CRC Press (Bocs Ration, FL).
|

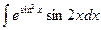
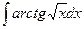
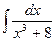
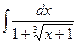
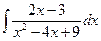

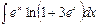




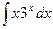
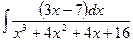



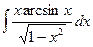




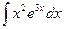



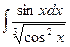
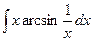
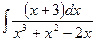
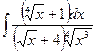


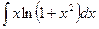
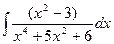
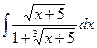
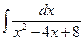




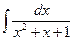
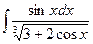

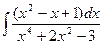
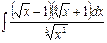
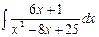
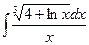
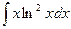
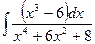
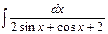



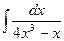

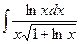
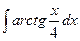


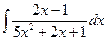
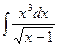

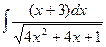



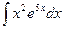
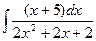
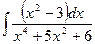
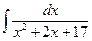

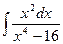

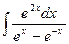
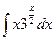
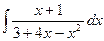






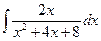
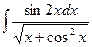


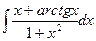


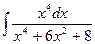
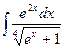

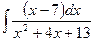





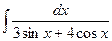
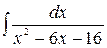
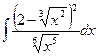

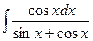
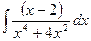


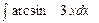


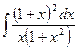
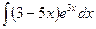
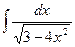
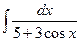
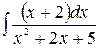

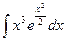
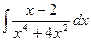

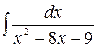
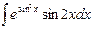
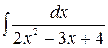
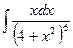
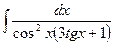
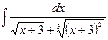
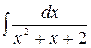


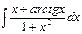
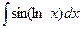
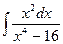
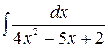


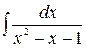
 б)
б) 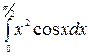
 б)
б) 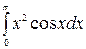
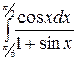 б)
б) 
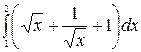 б)
б) 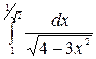
 б)
б) 
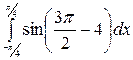 б)
б) 
 б)
б) 
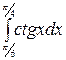 б)
б) 
 б)
б) 
 б)
б) 
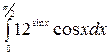 б)
б) 
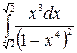 б)
б) 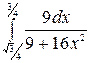
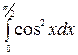 б)
б) 
 б)
б) 
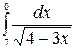 б)
б) 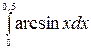
 б)
б) 
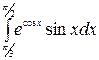 б)
б) 
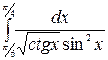 б)
б) 
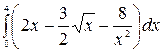 б)
б) 
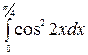 б)
б) 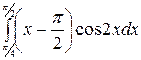
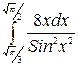 б)
б) 
 б)
б) 
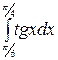 б)
б) 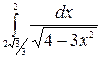
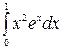
 б)
б)  б)
б) 
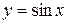 , the x-axis, and the lines
, the x-axis, and the lines  and
and  .
. .
. ,
,  for
for 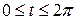 .
.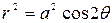 .
.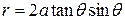 from
from  to
to  .
.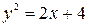 and the straight line
and the straight line 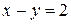 .
. .
.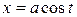 and
and 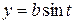 .
.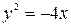 from (0,0) to (-4,4).
from (0,0) to (-4,4). , the x-axis, and the lines
, the x-axis, and the lines 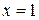 and
and  .
. and
and  .
.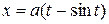 and
and 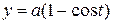 where
where 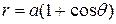 .
.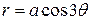 .
.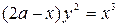 where
where  and its asymptote.
and its asymptote.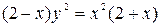 and find the area of the loop.
and find the area of the loop. , the coordinate axes, and the vertical line
, the coordinate axes, and the vertical line  .
.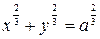 .
. and the lines x=0 and y=8.
and the lines x=0 and y=8.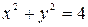 by the line y=1 is revolved about that line. Find the volume generated.
by the line y=1 is revolved about that line. Find the volume generated. and the parabola
and the parabola 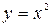 .
.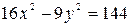 and the line x=6 is revolved about the y-axis. Find the volume generated.
and the line x=6 is revolved about the y-axis. Find the volume generated.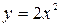 and the line
and the line  .
. about the initial line.
about the initial line. about the line
about the line  .
. ,
,  where
where  about the x-axis.
about the x-axis.


