Теорія Гуї - Чепмена
У 1910 р. Гуї і 1913 р. Чепмен незалежно один від одного розробили теорію будови подвійного електричного шару з дифузійним шаром протиіонів. В подвійному електричному шарі крім електростатичних сил діють також сили теплового руху, які прагнуть розподілити протиіони рівномірно в об’ємі. Біля твердої поверхні, на якій знаходяться потенціалвизначальні іони, переважають електростатичні сили, які прагнуть притягнути протиіони, тому їх концентрація тут велика. З відстанню дія цих сил зменшується і концентрація цих іонів теж зменшується і на деякій відстані стає рівною концентрації іонів в розчині. Ця відстань є товщиною подвійного електричного шару l (рис.40). Іони того ж знаку, що й потенціалвизначальні відштовхуються електростатичними силами від поверхні, тому їх концентрація тут значно менша і поступово зростає з відстанню. На великих відстанях від поверхні: с+ = с- =с∞
Рис. 40. Схема будови ПЕШ згідно теорії Гуї – Чепмена.
На малих відстанях від поверхні концентрація позитивних і негативних іонів описується законом розподілу Больцмана:
с ∞ - концентрація іонів в розчині; WX – робота по переміщенні іонів на відстань х від поверхні; z – заряд іона; jx – потенціал на відстані х від поверхні. Співвідношення між потенціалом j та об’ємною густиною заряду r для сферичного електричного поля визначається рівнянням Пуасона: ∂2j/∂x2 + ∂2j/∂y2 + ∂2j/∂z2 = -r/ea (5.18) Для плоского подвійного електричного шару можна розглядати змін потенціалу тільки по нормалі до поверхні, тому розглядаємо зміну потенціалу тільки по одній координаті: ∂2j/∂x2 = -r/ea (5.19) Об’ємну густину заряду можна представити, як: r = F(z+c+ - z-c-) (5.20) r = Fc∞Sziexp(jxziF/RT) (5.21) Підставимо це рівняння в рівняння Пуасона одержуємо рівняння Пуасона-Больцмана:
При малих значеннях потенціалу поверхні (j <25 мВ), (jxziF/RT)<< 1, розв’язок рівняння Пуасона-Больцмана має вигляд: jx = joe-c∙x (5.23) Де c згідно теорії сильних електролітів Дебая – Гюккеля величина обернена до товщини іонної атмосфери:
Для великих значень потенціалу (jxziF/RT)> 1
Згідно рівняння 5.21 заряд і потенціал поверхні взаємо пропорційні, тому ПЕШ можна вважати плоским конденсатором, відстань між пластинами якого дорівнює:
Товщина подвійного електричного шару зменшується з ростом концентрації іонів. Зростання температури приводять до збільшення швидкості руху іонів і збільшення товщини подвійного електричного шару. На відстані l потенціал поверхні jo зменшується в е=2,718 рази. jx = joe-cl = joe-c∙1/c = joe-1 = jo/e (5.28) При переміщені дисперсної фази відносно дисперсійного середовища межа ковзання знаходиться на якійсь відстані D від поверхні. Потенціал на межі ковзання називається електрокінетичним потенціалом, або z- (дзета) потенціалом. Величина z - потенціалу, на відміну від потенціалу поверхні jo, залежить від концентрації і валентності індиферентних іонів в розчині.
Рис. 41. Залежність потенціалу від відстані при різних концентраціях електроліту.
Теорія Гуї - Чепмена не враховує розміри іонів та вплив адсорбційних сил на структру ПЕШ. Це призвело до суттєвих розбіжностей між розрахунковими та експериментально визначеними параметрами ПЕШ та до неможливості пояснити явище перезарядки та різний вплив іонів з ліотропного ряду.
Приклад 5.1 Розрахуйте товщину дифузійного іонного шару на поверхні сульфату барію, що знаходиться в водному розчині NaOH з концентрацією 25 мг/л. Відносна діелектрична проникність розчину 82,2 при температурі 288 К. Розрахуємо молярну концентрацію розчину: c = 25∙10-3[г/л] /58,44 [г/моль] = 4,28∙10-4 моль/л = 0,428 моль/м3. Товщину дифузійного іонного шару розраховуємо за рівнянням λ = (εε0RT/ F2∑cz2)1/2 = = ((82,2∙8,85∙10-12∙8,314∙288)/(2 965002∙1/2 0,428(1∙12 + 1∙12)))1/2 = 1,477∙10-8 м = 14,77 нм. Приклад 5.2 Визначте значення потенціалу дифузійного шару для слабозарядженої поверхні на відстані 15 нм від поверхні. Середовище, що оточує поверхню - водний розчин NaCl з концентрацією 5∙10-4 моль/л, температура 293 К. Відносна діелектрична проникність середовища 80,1; потенціал поверхні 0,02 В. c = (F2∑cz2 / εε0RT)1/2 = (965002∙0,5(1∙12+1∙12) /∙80,1∙8,85∙10-12 8,314∙293)1/2 = = 73,43∙106 м-1 φx = φ0е-cx = 0,02∙е – 0,0734 ∙15∙ = 0,02∙е – 1,10 = 6,7 мВ Приклад 5.3 Розрахуйте ємність дифузійного шару дисперсної фази. Дисперсійне середовище – водний розчин СаСl2 з концентрацією 2∙10-4 моль/л і відносною діелектричною проникністю 83,8, при температурі 283 К. С = ε ε0/ λ = ε ε0 /(εε0RT / F2∑cz2)1/2 = = 83,8∙8,85∙10-12/(83,8∙8,85∙10-12∙8,314∙283/(965002∙0,2∙(22+2∙12)))1/2=59,4∙10-3 ф/м2
|


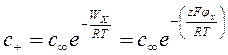 (5.16)
(5.16) (5.17)
(5.17) (5.22)
(5.22)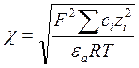 (5.24)
(5.24)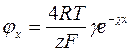 (5.25)
(5.25) (5.26)
(5.26)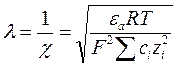 (5.27)
(5.27)



