Термодинамічні співвідношення між поверхневим натягом і електричним потенціалом
Утворення рівноважного подвійного електричного шару відбувається самочинно внаслідок переходу частини поверхневої енергії в електричну енергію. З об’єднаного виразу І-го і ІІ-го законів термодинаміки (2.1), при р,T,n=const: dG = sdS + jdq (5.1) Оскільки енергія Гіббса пропорційна екстенсивним величинам, то перейдемо від диференціалів функцій до самих функцій: G = s∙S + j∙q (5.2) Повний диференціал від енергії Гіббса дорівнює: dG = sdS + Sds + jdq + qdj (5.3) Якщо від рівняння (5.3) відняти (5.1), то отримаємо: Sds = -qdj (5.4)
де qs – заряд одиниці поверхні, або густина заряду. Вираз (5.5) має назву перше рівняння Ліпмана. Оскільки знак заряду поверхні і потенціалу завжди співпадають, то при зростання потенціалу поверхневий натяг завжди зменшується. Диференційна ємність ПЕШ, як і будь якого конденсатора дорівнює: Cd = dq/dj (5.6) Підставимо це вираз в перше рівняння Ліпмана і одержимо друге рівняння Ліпмана:
Друге рівняння Ліпмана дає можливість визначення ємності ПЕШ за залежністю поверхневого натягу від потенціалу. Якщо подвійний електричний шар являє собою плоский конденсатор, то його ємність: C = qs/j (5.8) qs = C∙j (5.9) Підставимо цей вираз в перше рівняння Ліпмана, одержуємо: ds/dj = -Cj (5.10) ds = -C∙jdj (5.11) про інтегруємо цей вираз:
при j0=0 одержуємо рівняння електрокапілярної кривої:
Рис. 38. Залежність поверхневого натягу від потенціалу поверхні.
Поверхневий натяг при зміні потенціалу змінюється за рівнянням параболи. Вершина параболи відповідає значенням j0 і smax, а сама парабола симетрична відносно осі ординат. В точці j0 і smax поверхневий шар має нульовий заряд, тобто ПЕШ відсутній. Стан, коли потенціал поверхні qs= 0, відповідає рівності хімічних потенціалів іонів в розчині і на твердій поверхні, що занурена в цей розчин. В 1883 р. Ліпман перевірив рівняння (5.14) на приладі власної конструкції, який він назвав капілярним електрометром, тому це рівняння одержало назву електрокапілярної кривої.
|

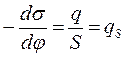 (5.5)
(5.5) (5.7)
(5.7) (5.12)
(5.12)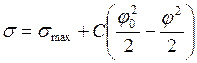 (5.13)
(5.13)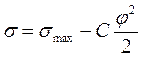 (5.14)
(5.14)



