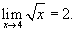Example 3
Using Cauchy definition, prove that
Let
the following inequality is valid:
We can write the last expression as
Hence,
Notice that our function takes only non-negative values. Therefore the ε -neighborhood at the given point must satisfy the condition ε ≤ 2. In this case the left side ε 2 − 4 ε of the inequality will be negative. It follows from here that
Thus, if we take δ ≤ 4 ε − ε 2, then for all x with
|

 .
.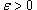 . We must find some number
. We must find some number  so that for all x with
so that for all x with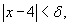
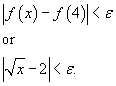
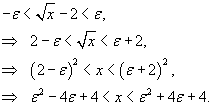


 , we will have
, we will have  . For example, if ε = 0.1, then the value of δ must be δ ≤ 4 ε − ε 2 = 0.4 − 0.01 = 0.39. This means, by Cauchy definition, that
. For example, if ε = 0.1, then the value of δ must be δ ≤ 4 ε − ε 2 = 0.4 − 0.01 = 0.39. This means, by Cauchy definition, that