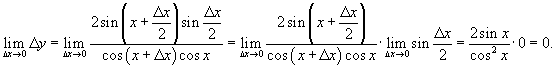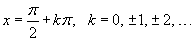Example 2
Using the Heine definition, show that the function
The secant function
where cosine is zero. Let Δ x be a differential of independent variable x. Find the corresponding differential of function Δ y.
Calculate the limit as
This result is valid for for all x except the roots of the cosine function:
Hence, the range of continuity and the domain of the function
|

 is continuous for any x in its domain.
is continuous for any x in its domain. has domain all real numbers x except those of the form
has domain all real numbers x except those of the form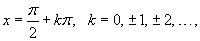
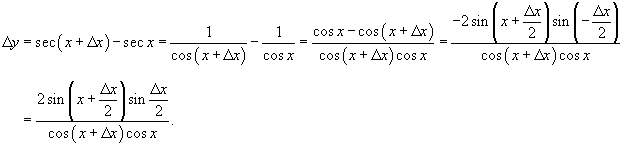
 .
.