Torque Produced in an Induction Motor
The torque in an induction motor results from the interaction of the revolving magnetic field of the stator with the currents induced in the conductors of the rotor winding. So the torque depends on both the stator magnetic flux Фт and the rotor current /2. But the process of energy conversion, i.e. production of the torque, involves only the active power consumed by the machine. That is why the torque actually depends on the active component of rotor current, I2 cosφ2, where φ2 is the phase angle between the emf and current in the rotor winding. The torque of an induction motor can thus be given by the expression T=сФтI2 cosφ2 where с is a constant accounting for the design features of the machine, i.e. the numbers of poles and phases, number of turns in the stator winding, and design of the rotor winding. Assuming that the externally applied voltage is constant, the magnetic flux also remains almost constant with any changes of the load on the shaft. In the expression for the torque, the flux Фm and с then do not vary and the torque is only proportional to the active component of I 2, T ~ I2 cosφ2. A change in the braking torque, i.e. the load on the rotor shaft, changes both the rotor speed and slip, which, in turn, causes a change both in the rotor current 12 and in its active component I 2cosφ2. The rotor current can be defined as the ratio of the emf to the impedance: I2 = E2Z2 = E2 The frequency of the rotor current changes with the value of slip. With the rotor stationary (n2 = 0 and S = 1), the flux of the revolving field threads the conductors of the stator and rotor windings at the same rate, therefore the rotor frequency is equal to the stator frequency, f2=f1. As the rotor starts running and the slip goes on decreasing, the conductors of the rotor winding cut the stator flux at a lower rate, with the result that the rotor frequency diminishes. When the rotor rotates in synchronism with the stator field (n2 = n1 and S = 0), the rotor conductors do not cut the stator flux and the rotor frequency is zero, f2 = 0. So, the rotor frequency is proportional to the slip, f2=Sf1, where Sf1 is the slip frequency. The rotor winding resistance is almost independent of frequency, whereas the emf and reactance are proportional to the rotor frequency, i.e. they vary with the value of slip: E2 = SE and X2 = SX, where E2 and X2 are respectively the emf and the reactance of the rotor winding at standstill. We thus can write: I2=SE/
Consequently, at low values of slip, approximately up to 20%, when SX is small as against R2, an increase in the slip causes the torque to grow because the active component I 2 cosφ2 of the rotor current increases. At large values of slip (SX > R2), an increase in the slip causes the torque to decrease because the reactance of the rotor winding grows appreciably.
Suppose that the propelling torque T is equal to the braking torque Tb at points A and B. If the operating conditions change for one reason or another and disturb the balance, the torques will gradually come to equilibrium in the first case and will not in the second. Assume that the torque has decreased due, for example, to a decrease in the supply voltage. The slip then begins to grow. If the equilibrium of torques is upset at point A, then an increase in the slip causes the torque to grow until it again becomes equal to the braking torque. If the equilibrium gets upset at point B, the growing slip will tend (to reduce the torque, which will remain smaller than the braking torque. The rotor speed will continuously decrease until the motor stops running. If the load torque applied to the motor shaft exceeds the breakdown torque, the motor will fail to restore the balance of torques and will stop. The torque produced by an induction motor varies as the square of the stator impressed voltage because both the magnetic flux and rotor current are proportional to this voltage. That is why changes in the voltage of the supply circuit heavily change the motoring torque.
|

 . The power factor is cosφ2= R2 Z2. Here R2, X2, and Z2 are the resistance, reactance, and impedance of the rotor winding.
. The power factor is cosφ2= R2 Z2. Here R2, X2, and Z2 are the resistance, reactance, and impedance of the rotor winding.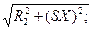 cosφ2=R2/
cosφ2=R2/ 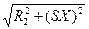 and T~I2cosφ2=SER2
and T~I2cosφ2=SER2 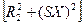 .
. Figure 7.6 illustrates the plot of torque versus slip. At a certain percentage slip Sm (about 20%), the motor develops a maximum torque Tm called the breakdown torque, which determines the overload capacity of the motor and is commonly equal to two or three times the rated torque. The motor can run steadily only within the ascending branch of the torque-slip curve, i.e. when the slip varies from 0 to Sm. The motor cannot operate within the descending branch, i.e. when S > Sm, because the steady equilibrium is impossible to attain in this slip range.
Figure 7.6 illustrates the plot of torque versus slip. At a certain percentage slip Sm (about 20%), the motor develops a maximum torque Tm called the breakdown torque, which determines the overload capacity of the motor and is commonly equal to two or three times the rated torque. The motor can run steadily only within the ascending branch of the torque-slip curve, i.e. when the slip varies from 0 to Sm. The motor cannot operate within the descending branch, i.e. when S > Sm, because the steady equilibrium is impossible to attain in this slip range.


