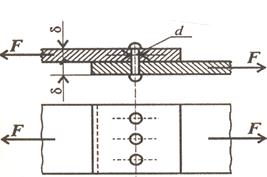
Running Conditions of an Induction Motor

As noted earlier, the running speed n₂ of the rotor of an induction motor is always less than the synchronous speed n₁ of the stator field revolving in the direction of the rotor. The revolving field thus slips with respect to the rotor and travels relative to it at a speed differential, n_s = n₁ – n₂, called the slip speed, or slip.

Slip is commonly expressed as a fraction of the synchronous speed, that is, as the ratio of the slip speed n_s to n₁:

S = n_s/n₁ = (n₁ — n₂₎/ln₁

At standstill when n₂ = 0, the per unit slip is equal to unity, or the percentage slip is equal to 100%. If the rotor revolves in synchro­nism with the field, n₂ = n_{1 ,} the slip is equal to zero. Thus, the higher the rotational speed of the rotor, the smaller the slip.

The slip of the rotor when running under load is usually small. In modern induction motors, the slip at full load reaches 3 to 5%, i.e. the rotor speed insignificantly differs from the synchronous speed. At no load, i.e. when the load on the shaft is absent, the value of slip is negligible and may be taken equal to zero.

The speed of the rotor can be defined from the following relations:

n₂ = n₁ — n_s = n(l — S) = (60f/p) (1 - S)

A motor will run steadily at a constant speed when the propelling torque T of the rotor is equal to the braking, or resisting, torque T_b of the shaft load such as a lathe tool. The rotor speed n₂ and slip S vary in a definite manner with the load on the shaft.

The stator field rotates with respect to the rotor at a definite slip speed n_s and induces an emf E₂ in the rotor winding, which forces the current I ₂ to circulate in the closed circuit of the rotor. An in­crease in the load, i.e. an increase in the resisting torque, disturbs the equilibrium of the torques since T_b becomes higher than T. The rotor slows down and the slip increases. The rate at which the rotor conductors cut the stator flux now grows, with the result that the emf E₂ increases accompanied by the corresponding increase in both the rotor current and the torque developed by the motor. The slip and the rotor current will continue to rise until the pro­pelling torque and the resisting torque become equal anew.

A similar process of variations in the rotor speed and the rotor torque occurs when the load on the shaft decreases. The braking torque then becomes smaller than the propelling torque and the rotor begins to gain speed, so the slip diminishes. The emf and, hence, the current in the rotor winding now fall off, causing the rotor torque to decrease until it again becomes equal to the braking torque.

The magnetic field of the stator links the conductors of the stator winding and induces in it the emf E₁ that balances out the impressed voltage V₁ of the supply circuit. Neglecting the voltage drop across the resistance of the stator winding, which is small in comparison with the emf, we can write an approximate equation V₁ = E₁.

Thus, if the impressed voltage does not vary in absolute value, the stator emf is approximately constant. The magnetic flux in the air gap of the machine, just like that in a transformer, is then nearly uniform, whatever the changes in loading.

The current in the rotor winding produces its own magnetic field which opposes the magnetic field produced by the current in the stator winding. In order that the resultant magnetic flux should remain constant at any load on the motor, the stator field must coun­terbalance the opposing rotor field. What enables the motor to keep the resultant flux constant is that as the current in the rotor winding grows, so too does the current in the stator winding.

An induction motor is thus simply a transformer with one of its windings revolving with respect to the other winding. As mentioned earlier, an increase in the secondary current of a transformer causes the primary current to increase too.