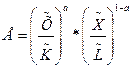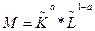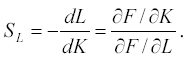Індивідуальне завдання №2
Виробнича фірма випускає продукцію із застосуванням праці робітників і основних засобів виробництва. Побудувати виробничу мультиплікативну регресію, оцінивши її параметри. Перевірити адекватність побудованої моделі вихідним даним. Зробити економічний аналіз параметрів виробничої функції. Визначити прогнозне значення випуску при Х1=160+К, Х2=200+К. Побудувати інтервал довіри прогнозу з надійністю 0,95. Оцінити ефективність і масштаб виробництва. На основі побудованої регресії розв’язати задачу оптимального випуску продукції: визначити, яка комбінація факторів виробництва є оптимальною, а також знайти максимальний об’єм випуску, якщо на витрати виробництва існує обмеження а 160 тис. грн., вартість оренди одиниці фондів складає 4+К тис. грн., вартість праці однієї людини – 1+К тис. грн. Побудувати ізокванту максимального випуску та ізокосту. Знайти графічний розв’язок задачі про комбінацію ресурсів і порівняти з аналітичним. Визначити граничну норму заміни одиниці фондів працею. Розв’язування
Для кожного показника таблиці – обсяг виробництва(У), показників витрат праці(Х1), капіталу (Х2) здійснюємо логарифмування - знаходимо логарифм натуральний. З метою перевірки адекватності моделі знаходимо функцію ЛИНЕЙН для прологарифмованих даних:
А0=1,79 Виходячи з даної статистики функція має вигляд: У=1,79*К0,17*L0,85 Перевіримо залежність параметрів а1 і а2 та визначимо їх економічний зміст: а1<а2, та при цьому (а1+а2)>1 (0,17+0,85 =1,02), можемо сказати, що підприємство має екстенсивне виробництво та економію ресурсів на масштабах виробництва. Тепер перевіримо адекватність моделі за допомогою F-критерію Фішера. Виходячи з статистичних таблиць Фішера для 5% рівня значимості та при ступенях вільності 1 та 9 знайдемо критичне значення. Після підрахунку показників можна прийти до висновку, що так як Fроз=47023,48>Fкр=5,32, то з надійністю 0,95 модна сказати, що побудована модель адекватна статистичним даним та з її допомогою можна проводити економічний аналіз. Перевіримо також статистичну значимість коефіцієнтів а0 та а1 за допомогою критерію Стьюдента. Так як t1=2,61>tкр=2,31 для параметру а1 та t2=9,67>tкр=2,31 для параметру а2, то ці параметри є статистично значимими. Розраховуємо прогнозне значення випуску при Х1=160+К та Х2=200+К. Після підрахунку показників можна прийти до висновку, що Упрог=391,02. ∆У розраховується за формулою:
Після підрахунку можемо зазначити, що ∆У = 280,36 Тому, верхня межа дорівнює 671,38, а нижня – 110,66. Для оцінки ефективності і масштабності виробництва застосовуємо таку формули:
Результати розрахунків:
Виробництво даного виду продукції є ефективним при даних співвідношеннях праці та капіталу, так як результат від діяльності більший за понесені затрати - коефіцієнти >1. Якщо має місце позитивний ефект масштабу, довгострокові середні витрати. Еластичність обсягу продукції зменшується при збільшенні витрати капіталу, та при збільшенні витрат праці на виготовлення даної продукції еластичність збільшується. Але при зміні капіталу на 1% темп приросту обсягу продукції буде більшим, аніж при зміні праці. На основі задачі розв’яжемо задачу оптимального випуску продукції. Аби знайти розв’язок задачі, необхідно перш за все скласти відповідні системи нерівності та обмежень Так, за умовою, вартість одиниці капіталу становить 11 у.о, а одиниць праці = 8у.о, а загальні затрати не повинні перевищувати 160 у.о: 8K+5L<=160 Виконавши розрахунки за рівнянням Лагранжа, можемо зазначити оптимальну комбінацію факторів виробництва: К=7, L=22, а Уmax=34,60. Ізокванта максимального випуску та ізокоста будуть мати такий вигляд:
Гранична норма заміщення капіталу працею розраховується за формулою: Визначається величиною капіталу, що її може замінити одиниця праці, не викликаючи при цьому зміни обсягу виробництва. Він показав, що на 73% зміниться співвідношення витрат капіталу і праці, якщо співвідношення їхніх граничних продуктів зміниться на 1 % (за інших рівних умов).
|