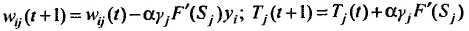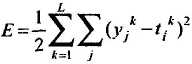Алгоритм обратного распространения ошибки и его недостатки

Данный алгоритм является эффек­тивным средством обучения многослойных нейронных сетей и представляет собой следующую последовательность шагов:

1. Задаются шаг обучения a (0<a<1) и желаемая среднеквадра­тичная ошибка нейронной сети Е_m.

2. Инициализируются случайным образом весовые коэффициен­ты и пороговые значения нейронной сети.

3. Подаются последовательно образы из обучающей выборки на вход нейронной сети и для каждого входного образа выпол­няются следующие действия:

3.1. Производится фаза прямого распространения входного образа по нейронной сети. При этом вычисляется выходная активность всех нейронов сети

где индекс j характеризует нейроны следующего слоя по отноше­нию к слою i.

3.2. Осуществляется фаза обратного распространения сигнала, в результате которой определяется ошибка g_j , j = 1,2,... нейронных эле­ментов для всех слоев сети. При этом для выходного слоя g_j = y_j - t_j, а для скрытого слоя

3.3. Изменяются веса и пороги нейронов для каждого слоя нейронной сети:

4. Вычисляется суммарная среднеквадратичная ошибка ней­ронной сети

где L – размерность обучающей выборки.

5. Если Е > Е_m, то происходит переход к шагу 3 алгоритма. В противном случае алгоритм обратного распространения ошибки заканчивается.

Таким образом, данный алгоритм функционирует до тех пор, пока суммарная среднеквадратичная ошибка сети не станет меньше заданной, т.е. Е £ Е_m.

Алгоритм обратного распространения ошибки, основанный на методе градиентного спуска, имеет следующие недостатки:

ü неизвестность выбора числа слоев и количества нейронов в слое;

ü медленная сходимость гра­диентного метода с постоянным шагом обучения;

ü сложность выбора подходя­щей скорости обучения a: слишком малое a увеличивает время обучения и приводит к скатыванию нейронной сети в локальный минимум, большое a может привести к пропуску глобального минимума и сделать процесс обучения расходящимся;

ü невозможность определения точек локального и глобального ми­нимумов, так как градиентный метод их не различает;

ü влияние случайной инициализации весовых коэффициентов нейронной сети на поиск минимума функции среднеквадра­тичной ошибки.

Последний пункт отражает, что при разной инициализации могут получаться различные решения задачи. Это характеризует неустойчивость алгоритма обучения. То, что алгоритм не позволяет в общем случае достичь глобального мини­мума, не уменьшает его достоинств, так как во многих практических задачах достаточно обучить нейронную сеть до требуемой среднеквадратичной ошибки. Является ли при этом найденный минимум локальным или глобальным, не имеет большого значения.