Использование линейной нейронной сети для прогнозирования
Способность нейронных сетей после обучения к обобщению и пролонгации результатов создает потенциальные предпосылки для построения на их базе различного рода прогнозирующих систем. Рассмотрим прогнозирование временных рядов при помощи линейных нейронных сетей. Пусть дан временной ряд x(t) на промежутке
Совокупность известных значений временного ряда образует обучающую выборку, размерность которой характеризуется значением m. Для прогнозирования временных рядов используется метод «скользящего окна». Он характеризуется длиной окна р, равной числу элементов ряда, одновременно подаваемых на нейронную сеть. Это определяет структуру нейронной сети, которая состоит из р распределительных нейронов и одного выходного нейрона. Такая модель соответствует линейной авторегрессии и описывается как
где wk – весовые коэффициенты нейронной сети; Ошибка прогнозирования определяется выражением е (n) = x (n) - Модель линейной авторегрессии формирует значение ряда x (n), как взвешенную сумму предыдущих значений ряда. Обучающую выборку нейронной сети можно представить в виде матрицы, строки которой характеризуют векторы, подаваемые на вход сети:
Это эквивалентно перемещению окна по ряду x (t) с единичным шагом. Таким образом, для обучения нейронной сети прогнозированию используется выборка известных членов ряда. После обучения сеть должна прогнозировать временной ряд на упреждающий промежуток времени.
|
. Тогда задача прогнозирования состоит в том, чтобы найти продолжение временного ряда на неизвестном промежутке, т.е. необходимо определить x (m +1), x (m +2) и т.д.
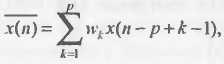
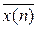– оценка значения ряда x (n) в момент времени n.
