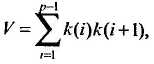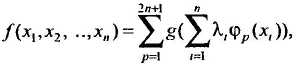Многослойные нейронные сети
Многослойная нейронная сеть способна осуществлять любое отображение входных векторов в выходные. Это свойство многослойных нейронных сетей отмечали ещё в 60-х годах М.Минский и С.Пайперт. Однако на тот момент времени не было эффективного алгоритма обучения таких сетей. Поэтому их выводы по перспективам развития многослойных нейронных сетей были весьма пессимистичными. В 1986 г. рядом авторов (Rumelhart, Hinton, Williams) независимо друг от друга был предложен алгоритм обратного распространения ошибки, который стал эффективным средством обучения многослойных нейронных сетей.
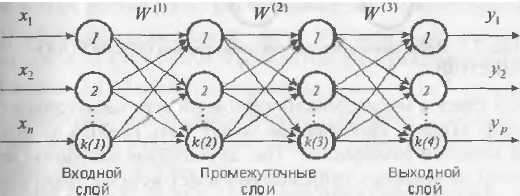
Архитектура многослойной НС состоит из множества слоев нейронов.
Входной слой (input layer) выполняет распределительные функции. Выходной слой (output layer) служит для обработки информации от предыдущих слоев и выдачи результатов. Слои, расположенные между входным и входным, называются промежуточными или скрытыми (hidden layers). Как и выходной слой, скрытые слои являются обрабатывающими. Выход каждого нейрона предыдущего слоя сети соединен синаптическими связями со всеми входами нейронов следующего слоя. В качестве функции активации нейронных элементов обычно используется гиперболический тангенс или сигмоидная функция. Пусть W ( i ) – матрица весовых коэффициентов i -го слоя многослойной сети. Тогда для нейронной сети с двумя скрытыми слоями выходные значения Y = F (F (F (XW (1)) W (2)) W (3)) где X =(x1,x2,...,xn) – вектор-строка входных сигналов; F – функция активации. Общее число синаптических связей многослойной нейронной сети
где р – общее количество слоев сети; k (i) – количество нейронов в i -м слое. Число слоев в многослойной нейронной сети характеризует, каким образом входное пространство может быть разбито на подпространства меньшей размерности. Так, двухслойная нейронная сеть с одним слоем нелинейных нейронов разбивает входное пространство образов на классы при помощи гиперплоскости. Трехслойная нейронная сеть, где в качестве двух последних слоев используются нейронные элементы с нелинейной функцией активации, позволяет формировать любые выпуклые области в пространстве решений. Четырехслойная нейронная сеть, которая имеет три нелинейных слоя, дает возможность получать область решений любой формы и сложности, в том числе и невыпуклой. В 1957 г. А.Н. Колмогоров показал, что любую непрерывную функцию n переменных на единичном отрезке [0,1] можно представить в виде суммы конечного числа одномерных функций:
где функции g и j p являются одномерными и непрерывными; l i = const " i. Данная теорема легла в основу построения многослойных НС для аппроксимации функций. Из нее следует, что любую непрерывную функцию f:[0,1] n ® [0,1] можно аппроксимировать при помощи трехслойной нейронной сети, которая имеет n входных, (2 n + 1) скрытых и один выходной нейрон. Однако проблема здесь состоит в выборе соответствующих функций g и j. В 1988 г. ряд авторов обобщили приведенные выше результаты на многослойную нейронную сеть с алгоритмом обратного распространения ошибки. Теорема. Любая непрерывная функция f:[0,1]n ® [0,1] может быть аппроксимирована трехслойной нейронной сетью с одним скрытым слоем и алгоритмом обратного распространения ошибки с любой степенью точности. Данная теорема является основной для аппроксимации функций при помощи многослойных нейронных сетей.
|