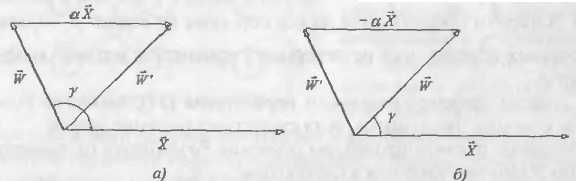
Геометрическая интерпретация процедуры обучения персептрона
Представим взвешенную сумму нейронной сети в виде скалярного произведения весового вектора на входной вектор: S = (W, X) = |W| |X| cos g, где g – угол между векторами W и X. Тогда, если 0<g<90°, то S>0 и у=1. Если 90°£g<180°, то S£0 и у=0. Рассмотрим векторы W и X. Пусть угол между ними g³90° (рис. а). В этом случае S£0 и у=0. Предположим, что эталонное значение t=1. Тогда вектор W необходимо преобразовать таким образом, чтобы угол g стал меньше 90°. Отсюда правило преобразования вектора W будет следующим: W' = W + aX Рассмотрим другой случай (рис. б). Пусть g<90°. Тогда S>0 и у=1. Предположим, что эталонное значение t=0. Тогда вектор W необходимо преобразовать так, чтобы угол g стал больше 90°. Правило преобразования можно представить как W' = W - aX
Пусть W' = W(t+1), a W = W(t). Тогда, объединяя приведенные выше два правила в одно, получим следующее выражение для настройки весовых коэффициентов: W(t+l) = W(t)-a(y-t)X = W(t) + a(t-y)X. Это выражение характеризует правило обучения Розенблатта в общей форме.
|