Структура и свойства искусственного нейрона
Искусственный нейрон состоит из элементов трех типов: умножителей (синапсов), сумматора и нелинейного преобразователя. Синапсы осуществляют связь между нейронами, умножают входной сигнал на число, характеризующее силу связи (вес синапса). Сумматор выполняет сложение сигналов, поступающих по синаптическим связям от других нейронов, и внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента - выхода сумматора. Эта функция называется функцией активации или передаточной функцией. Рассмотрим модель искусственного нейрона.
Математическая модель нейрона может быть представлена выражением
где Если сила связи wj отрицательная, то такая связь называется тормозящей. В противном случае она является усиливающей (возбуждающей). В общем случае входной сигнал, весовые коэффициенты и смещение могут принимать действительные значения. Выход (у) определяется видом функции активации и может быть как действительным, так и целым. На входной сигнал s нелинейный преобразователь отвечает выходным сигналом y=f(s), представляющим собой выход нейрона.
Примеры активационных функций а – функция единичного скачка; б – линейный порог (гистерезис) в – сигмоида (логистическая ф-я); г – сигмоида (гиперболический тангенс) Одной из наиболее распространенных является логистическая функция или сигмоида (функция S-образного вида):
При уменьшении параметра а сигмоида становится более пологой, в пределе при а=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении а сигмоид приближается к виду функции единичного скачка с порогом Q. Из выражения для сигмоиды очевидно, что выходное значение нейрона лежит в диапазоне (0, 1). Одно из ценных свойств сигмоидальной функции - простое выражение для ее производной, применение которой будет рассмотрено в дальнейшем:
Следует отметить, что сигмоидальная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Кроме того, она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоида имеет пологий наклон.
|

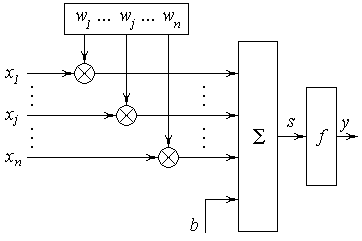
 ,
, – входной сигнал нейрона;
– входной сигнал нейрона;  – вес синаптической связи; b – смещение (порог) нейрона; s – результат суммирования входных сигналов; y – выходной сигнал нейрона; n – число входов нейрона; f – функция активации.
– вес синаптической связи; b – смещение (порог) нейрона; s – результат суммирования входных сигналов; y – выходной сигнал нейрона; n – число входов нейрона; f – функция активации.






