Классификация нейронных сетей и их свойства

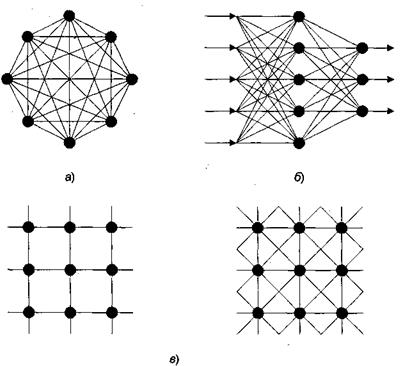
Нейронная сеть представляет собой совокупность нейронных элементов, определенным образом соединенных друг с другом и с внешней средой с помощью связей, определяемых ве­совыми коэффициентами. В зависимости от функциональности выделяют три типа нейронов в нейронной сети:

- входные нейроны, на которые подается вектор входных сигналов;

- выходные нейроны, выходные значения которых представляют выходы НС;

- промежуточные нейроны, составляющие основу нейронных сетей.

В большинстве моделей НС тип нейрона связан с его расположением в сети. Если нейрон имеет только выходные связи, то это входной нейрон, если наоборот - выходной нейрон. Однако возможен случай, когда выход топологически внутреннего нейрона рассматривается как часть выхода сети. В целом процессе функциониро­вания сети осуществляется преобразование входного вектора сигналов в выходной.

Конкретный вид выполняемого сетью преобразования данных обусловливается не только характеристиками нейронных элементов, но и особен­ностями архитектуры НС, а именно топологией межнейронных свя­зей, выбором определенных нейронных элемен­тов для ввода и вывода информации, способами обучения сети, наличием или отсутствием конкуренции между нейронами, на­правлением и способами управления и синхронизации передачи информации между нейронами.

С точки зрения топологии можно выделить три основных ти­па НС:

а) полносвязные; б) многослойные; в) слабосвязные.

В полносвязных нейронных сетях каждый нейрон передает свой выходной сигнал остальным нейронам, в том числе и самому себе. Все входные сигналы подаются всем нейронам. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети.

В многослойных нейронных сетях нейроны объединяются в слои. Слой содержит совокупность нейронов с едиными входными сигналами. Число нейронов в слое может быть любым и не зави­сит от количества нейронов в других слоях. В общем случае сеть состоит из Q слоев, пронумерованных слева направо. Внешние входные сигналы подаются на входы нейронов входного слоя (его часто нумеруют как нулевой), а выходами сети являются выходные сигналы последнего слоя. Кроме входного и выходного слоев в многослойной нейронной сети есть один или несколько скрытых слоев. Связи от выходов нейронов некоторого слоя q к входам нейронов следующего слоя (q+1) называются последовательными.

Среди многослойных нейронных сетей вы­деляют следующие типы.

1) Монотонные. Это частный случай многослойных сетей с дополнительными ус­ловиями на связи и нейроны. Каждый слой кроме вы­ходного разбит на два блока: возбуждающий и тормозящий. Связи между блоками тоже разделяются на тормозящие и возбуждаю­щие. Если от нейронов блока А к нейронам блока В ведут только возбуждающие связи, то это означает, что любой выходной сигнал блока является монотонной неубывающей функцией любого вы­ходного сигнала блока А. Если же эти связи только тормозящие, то любой выходной сигнал блока В является невозрастающей функ­цией любого выходного сигнала блока А. Для нейронов монотон­ных сетей необходима монотонная зависимость выходного сигна­ла нейрона от параметров входных сигналов.

2) Сети без обратных связей. В таких сетях нейроны вход­ного слоя получают входные сигналы, преобразуют их и передают нейронам первого скрытого слоя, и так далее вплоть до выходного слоя. Среди сетей данного типа различают полносвязанные (выход каждого нейрона q-ro слоя связан с входом каждого нейрона (q+1)-го слоя) и частично полносвязанные.

Пример многослойной (двухслойной) сети прямого распространения.

3) Сети с обратными связями. В таких сетях информация с последующих слоев передается на предыдущие.

Пример: частично-рекуррентные сети Элмана (а) и Жордана (б).

В слабосвязных нейронных сетях нейроны располагаются в узлах прямоугольной или гексагональной решетки. Каждый нейрон связан с четырьмя (окрестность фон Неймана), шестью (окрест­ность Голея) или восемью (окрестность Мура) своими ближайшими соседями.

Нейронные сети можно разделить по типам струк­тур нейронов на гомогенные (однородные) и гетерогенные. Гомо­генные сети состоят из нейронов одного типа с единой функцией активации, а в гетерогенную сеть входят нейроны с различными функциями активации.

Выбор структуры нейронной сети осуществляется в соответ­ствии с особенностями и сложностью задачи. Для решения от­дельных типов задач уже существуют оптимальные конфигурации НС. Если же задача не может быть сведена ни к одному из известных типов, приходится решать сложную про­блему синтеза новой архитектуры. При этом необходимо руково­дствоваться следующими правилами:

- возможности сети возрастают с увеличением числа нейронов сети, плотности связей между ними и числа слоев;

- введение обратных связей наряду с увеличением возможностей сети поднимает вопрос о динамической устойчивости сети;

- сложность алгоритмов функционирования сети, введение нескольких типов синапсов способствует усилению мощности нейронной сети.

Вопрос о необходимых и достаточных свойствах сети для решения задач того или иного рода представляет собой целое на­правление нейрокомпьютерной науки. Так как проблема синтеза нейронной сети сильно зависит от решаемой задачи, дать общие подробные рекомендации затруднительно. В большинстве случаев оптимальный вариант получается на основе интуитивного подбо­ра, хотя в литературе приведены доказательства того, что для лю­бого алгоритма существует нейронная сеть, которая может его реализовать.

Многие задачи распознавания образов (зрительных, рече­вых), выполнения функциональных преобразований при обработке сигналов, управления, прогнозирования, идентификации сложных систем, сводятся к следующей математической постановке. Необ­ходимо построить такое отображение X -> У, чтобы на каждый возможный входной сигнал X формировался правильный выход­ной сигнал Y. Отображение задается конечным набором пар (<вход>, <известный выход>). Число этих пар (обучающих приме­ров) существенно меньше общего числа возможных сочетаний значений входных и выходных сигналов. Совокупность всех обу­чающих примеров носит название обучающей выборки.

В задачах распознавания образов X - некоторое представ­ление образа (изображение, вектор), У - номер класса, к которому принадлежит входной образ.

В задачах управления X - набор контролируемых парамет­ров управляемого объекта, У - код, определяющий управляющее воздействие, соответствующее текущим значениям контролируе­мых параметров.

В задачах прогнозирования в качестве входных сигналов ис­пользуются временные ряды, представляющие значения контро­лируемых переменных на некотором интервале времени. Выход­ной сигнал - множество переменных, которое является подмноже­ством переменных входного сигнала.

Вообще говоря, большая часть прикладных задач может быть сведена к реализации некоторого сложного функционального многомерного преобразования X -> У, при котором необходимо обеспечить формирование правильных выходных сигналов нейронной сети в соответствии со всеми примерами из обучающей выборки.