Правило обучения Хебба

Самоадаптация и самоорганизация нейронных сетей достигаются в процессе их обучения, в ходе которого определяются синаптические связи между нейронными элементами. Обучающие правила определяют, как изменяются весовые коэффициенты в ответ на входное воздействие.

Правило обучения Хебба имеет биологические предпосылки. Оно является основой многих методов обучения нейронных сетей. Согласно этому правилу, обучения происходит в результате усиления силы связи между одновременно активными нейронами. Поэтому часто используемые в сети связи усиливаются, что объясняет феномен обучения путём повторения и привыкания.

Пусть имеются два нейрона i и j, между которыми существует сила связи w_ij.

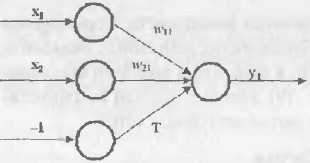
Тогда правило обучения Хебба можно записать следующим образом:

w_ij (t +1) = w_ij (t) + x_i y_j

где t – время x_i и y_j – соответственно выходы i -го и j -го нейронов.

В начальный момент времени предполагается, что w_ij (t =0) = 0, " i, j.

Рассмотрим применение правила Хебба для простейшей нейронной сети, состоящей из двух входных и одного выходного нейрона.

В такой сети порог выходного нейрона является скрытым в этом элементе. При операциях с нейронными сетями порог нейрона можно вынести за его пределы и изобразить как синаптическую связь с весом, равным T. Так как входное значение, подаваемое на дополнительный нейрон, равно -1, то взвешенная сумма

S=w₁₁x₁ + w₂₁x₂ - T₁

Обучение нейронной сети происходит путём настройки весовых коэффициентов и порогов нейронов. Правило обучения Хебба запишется в виде выражений:

w₁₁ (t +1) = w₁₁ (t) + x₁ y₁

w₂₁ (t +1) = w₂₁ (t) + x₂ y₁

T (t +1) = T (t) - y₁

Аналогично правило Хебба записывается для НС большей размерности.

Обучение заканчивается после подачи всех входных образов на сеть.