Однослойная нейронная сеть с пороговой функцией активации
Рассмотрим нейронную сеть, состоящую из одного слоя нейронных элементов, который осуществляет обработку входной информации. Такую сеть принято изображать в виде двухслойной нейронной сети, где первый слой является распределительным, а второй – обрабатывающим. При этом каждый нейрон первого слоя имеет синаптические связи со всеми нейронами второго слоя.
Тогда выходное значение j -го нейрона второго слоя можно представить как
где Tj – порог j -го нейрона выходного слоя; wij – сила синаптич. связи между i -м нейроном распределительного слоя и j -м нейроном обрабатывающего слоя. Совокупность весовых коэффициентов сети можно представить в виде матрицы размерностью n ´ m:
Тогда вектор-столбец взвешенной суммы в матричном виде определяется как: S = WT X - T где Т – вектор-столбец порогов нейронов второго слоя. Рассмотрим нейронную сеть с двумя нейронами входного и одним нейроном выходного слоя.
Взвешенная сумма S=w11x1 + w21x2 - T1 Соответственно выходное значение нейронной сети
Такая есть осуществляет линейное разделение входного пространства сигналов на два класса и может использоваться для решения задачи классификации образов. При этом уравнение разделяющей линии w11x1 + w21x2 - T1 = 0 Она разделяет область решений, соответствующую одному классу, от другого класса и называется дискриминантной линией. Имеем
В системе координат (x1, x2) данное уравнение изображает прямую линию (дискриминантную линию), которая отделяет один класс от другого.
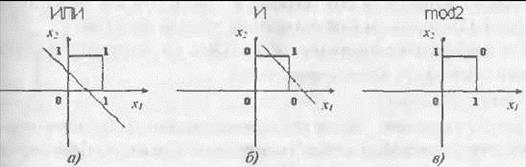
При этом величина Если размерность входного сигнала n=3, то разделяющей поверхностью будет плоскость; если n>3 – гиперплоскость. Рассмотрим решение простейших задач логических операций на такой сети. Эти задачи решаются с использованием нейронной сети, если их пространство решений можно разбить на два класса.
а) решение логической задачи ИЛИ; б) И; в) ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR). Видно, что рассмотренная нейронная сеть может решить задачу типа И и ИЛИ, но неспособна решить задачу ИСКЛЮЧАЮЩЕЕ ИЛИ. Таким образом, линейная разделяющая поверхность, формируемая нейронной сетью с одним слоем обрабатывающих нейроннов, ограничивает круг решаемых задач. Это показали американские ученые М. Минский и С. Пайперт, которые сделали пессимистические выводы насчет дальнейшего развития нейронных сетей.
|



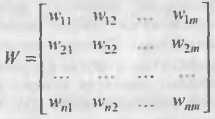



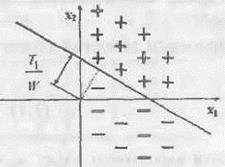
 представляет собой расстояние от центра координат до прямой. Тогда, если XW >
представляет собой расстояние от центра координат до прямой. Тогда, если XW >