Правило обучения Видроу-Хоффа
Используется для обучения нейронной сети, состоящей из распределительных нейронов и одного выходного нейрона, имеющего линейную функцию активации.
Такая сеть называется адаптивным нейронным элементом или ADALINE (Adaptive Linear Element). Выходное значение такой сети
Правило обучения Видроу-Хоффа известно под названием дельта-правило (delta rule). Оно предполагает минимизацию среднеквадратичной ошибки нейронной сети, которая для L входных образов определяется следующим образом:
где Е(к) – среднеквадратичная ошибка сети для k -го образа; Среднеквадратичная ошибка нейронной сети для одного входного образа определяется по формуле
Правило обучения Видроу-Хоффа базируется на методе градиентного спуска в пространстве весовых коэффициентов и порогов нейронной сети. Согласно этому правилу веса и пороги нейронной сети необходимо изменять с течением времени по следующим выражениям:
Найдем производные ошибки E по параметрам сети wj1 и Т:
где Отсюда получаем выражения для обучения нейронной сети по дельта-правилу: wjl (t + l) = wjl (t) - a( T (t + l) = T (t) + a( Б. Видроу и М. Хофф доказали, что данный закон обучения всегда позволяет находить весовые коэффициенты нейрона таким образом, чтобы минимизировать среднеквадратичную ошибку сети независимо от начальных значений весов. Алгоритм обучения, в основе которого лежит дельта-правило, состоит из следующих шагов: 1. Задаются скорость обучения a (0<a<1) и минимальная среднеквадратичная ошибка сети Еm, которой необходимо достичь в процессе обучения. 2. Случайным образом инициализируются весовые коэффициенты и порог нейронной сети. 3. Подаются входные образы на нейронную сеть и вычисляются векторы выходной активности сети. 4. Осуществляется изменение весовых коэффициентов и порога нейронной сети согласно правилам обучения. 5. Алгоритм продолжается до тех пор, пока суммарная среднеквадратичная ошибка сети не станет меньше заданной, т. е. Е £ Еm. В алгоритме Видроу-Хоффа существует проблема выбора значения шага обучения a. Если шаг a слишком мал, то процесс обучения является очень длительным; если a большой, процесс обучения может оказаться расходящимся, т.е. не привести к решению задачи. Т.о., сходимость алгоритма обучения зависит от разумного выбора значения шага обучения. В некоторых работах предполагается выбирать значение a, которое уменьшается в процессе обучения следующим образом:
где k – номер итерации в алгоритме обучения.
|

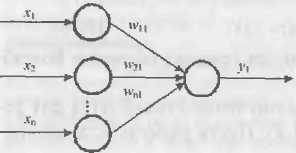

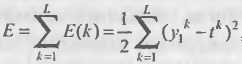
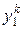 и tk – соответственно выходное и эталонное значения нейронной сети для k -го образа.
и tk – соответственно выходное и эталонное значения нейронной сети для k -го образа.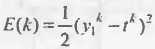



 – j -я компонента k -го образа.
– j -я компонента k -го образа.



