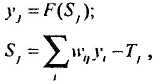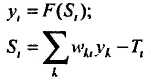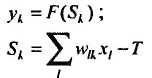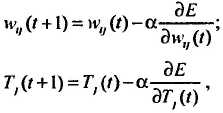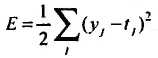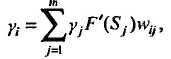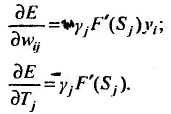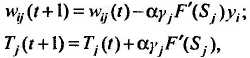Математические основы алгоритма обратного распространения ошибки

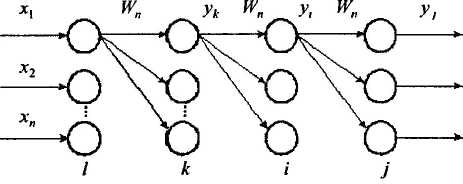
Алгоритм обратного распространения ошибки был предложен D.Rumelhart, G.Hinton, R.Williams в 1986 г. и является эффективным средством для обучения многослойных нейронных сетей.

Рассмотрим нейронную сеть, состоящую из четырех слоев.

Обозначим слои нейронных элементов от входа к выходу соответственно через l, k, i, j. Тогда выходное значение j -го нейрона последнего слоя

где S_j – взвешенная сумма j -го нейрона выходного слоя; у_i – выход­ное значение i -го нейрона предпоследнего слоя; w_ij и T_j – соответст­венно весовой коэффициент и порог j -го нейрона выходного слоя.

Аналогично выходное значение i -го нейрона предпо­следнего слоя

Соответственно для k -го слоя

Алгоритм обратного распространения ошибки минимизирует среднеквадратичную ошибку нейронной сети. Для этого с целью на­стройки синаптических связей используется метод градиентного спуска в пространстве весовых коэффициентов и порогов нейронной сети. Со­гласно методу градиентного спуска изменение весовых коэффициентов и порогов нейронной сети происходит по следующему правилу:

где Е – среднеквадратичная ошибка нейронной сети для одного образа.

где t_j – эталонное выходное значение j -го нейрона.

Ошибка j -го нейрона выходного слоя g_j = y_j - t_j.

Теорема. Для любого скрытого слоя i ошибка i-го нейронно­го элемента определяется рекурсивным образом через ошибки нейро­нов следующего слоя j:

где m – число нейронов следующего слоя по отношению к слою i; w_ij – синаптич. связь между i -м и j -м нейронами различных слоев; S_j – взвеш. сумма j -го нейрона.

Используя результаты данной теоремы, можно определить ошибки нейронов скрытого слоя через ошибки нейронов следующего слоя по отношению к скрытому.

Теорема. Производные среднеквадратичной ошибки по весо­вым коэффициентам и порогам нейронных элементов для любых двух слоев i и j многослойной сети определяются следующим образом:

Следствие. Для минимизации среднеквадратичной ошибки сети весовые коэффициенты и пороги нейронных элементов должны изменяться с течением времени следующим образом:

где a – скорость обучения.

Данное следствие определяет правило обучения многослойных нейронных сетей в общем виде, которое называется обобщенным дельта-правилом.