Основная теорема о генетических алгоритмах
Основная теорема, относящаяся к генетическим алгоритмам, называется теоремой о схемах [23]. Понятие схема используется для определения множества хромосом, обладающих некоторыми общими свойствами, т.е. подобных друг другу. Если аллели принимают значения 0 или 1 (рассматриваются хромосомы с двоичным алфавитом), то схема представляет собой множество хромосом, содержащих нули и единицы на некоторых заранее определенных позициях. При рассмотрении схем удобно использовать алфавит {0, 1, *}, в который помимо 0 и 1 введен дополнительный символ *, обозначающий любое допустимое значение, т.е. 0 или 1. Например, 10*1={1001, 1011} *01*10={001010, 001110, 101010, 101110} Говорят, что хромосома принадлежит к данной схеме, если для любой j -й позиции (локуса), j = 1, 2,..., L (где L – длина хромосомы) символ, занимающий j -ю позицию хромосомы, соответствует символу, занимающему j -ю позицию схемы, причем символу * соответствуют как 0, так и 1. Отметим, что если в схеме присутствует т символов *, то эта схема содержит 2 m хромосом. А каждая хромосома (цепочка) длиной L принадлежит к 2 L схемам. Для примера в таблице 7.1 приведены схемы для цепочки длиной 2. Табл. 7.1. Схемы, к которым принадлежат цепочки длиной 2
Генетический алгоритм базируется на принципе трансформации наиболее приспособленных особей (хромосом). Пусть Р (0) означает исходную популяцию особей, а Р (k) – текущую популяцию (на k -й итерации алгоритма). Из каждой популяции Р (k), k = 0, 1,... методом селекции выбираются хромосомы с наибольшей приспособленностью, которые включаются в родительский пул M (k). Далее, в результате объединения особей из популяции M (k)в родительские пары и выполнения операции скрещивания с вероятностью р с, а также операции мутации с вероятностью рт формируется новая популяция Р (k+ 1), в которую входят потомки особей из популяции M (k). Следовательно, для любой схемы, представляющей хорошее решение, было бы желательным, чтобы количество хромосом, соответствующих этой схеме, возрастало с увеличением количества итераций k. На соответствующее преобразование схем в генетическом алгоритме оказывают влияние 3 фактора: селекция хромосом, скрещивание и мутация. Проанализируем воздействие каждого из них с точки зрения увеличения ожидаемого количества представителей отдельно взятой схемы. Обозначим рассматриваемую схему символом S, а количество хромосом популяции Р (k), соответствующих этой схеме – c(S, k). Следовательно, c(S, k) – есть количество элементов (мощность) множества Р (k)Ç S. Исследуем влияние селекции. При выполнении этой операции хромосомы из популяции Р (k) копируются в родительский пул М (k)с вероятностью, определяемой выражением
Пусть F (S, k) обозначает среднее значение функции приспособленности хромосом из популяции Р (k), которые соответствуют схеме S. Если
то
Величина F (S, k)также называется приспособленностью схемы S на k -й итерации. Пусть Á(k) обозначает сумму значений функций приспособленности хромосом из популяции P (k) мощностью N, т.е.
Обозначим через
Пусть
Таким образом, ожидаемое количество хромосом из множества Р (k)Ç S, отобранных для включения в родительский пул М (k), будет равно
Поскольку каждая хромосома из родительского пула М (k)одновременно принадлежит популяции Р (k), то хромосомы, составляющие множество M (k)Ç S –это те же самые особи, которые были отобраны из множества Р (k)Ç S для включения в популяцию M (k). Если количество хромосом родительского пула M (k), соответствующих схеме S (т.е. количество элементов множества M (k)Ç S), обозначить b (S, k), то из этих рассуждений можно сделать следующий вывод. Вывод 1 (влияние селекции) Ожидаемое значение b (S, k), т.е. значение количества хромосом родительского пула M (k), соответствующих схеме S, определяется выражением
Из этого следует, что если схема S содержит хромосомы со значением функции приспособленности, превышающим среднее значение, то ожидаемое количество хромосом из родительского пула M (k), соответствующих схеме S, будет больше количества хромосом из популяции Р (k), соответствующих схеме S. Поэтому можно утверждать, что селекция вызывает распространение схем с приспособленностью «лучше средней» и исчезновение схем с «худшей» приспособленностью. Прежде чем приступить к анализу влияния генетических операторов скрещивания и мутации на хромосомы из родительского пула, определим необходимые для дальнейших рассуждений понятия порядка и охвата схемы. Пусть L обозначает длину хромосом, соответствующих схеме S.
|

 .
.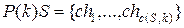 ,
, .
.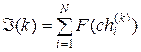 .
. среднее значение функции приспособленности хромосом этой популяции, т.е.
среднее значение функции приспособленности хромосом этой популяции, т.е.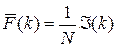 .
. обозначает элемент родительского пула М (k). Для каждого
обозначает элемент родительского пула М (k). Для каждого 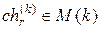 и для каждого i =1,…, c (S, k)вероятность того, что
и для каждого i =1,…, c (S, k)вероятность того, что  определяется отношением F (ch i) / F (k). Поэтому ожидаемое количество хромосом в популяции М (k), которые равны ch i, составит
определяется отношением F (ch i) / F (k). Поэтому ожидаемое количество хромосом в популяции М (k), которые равны ch i, составит .
.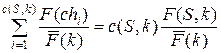 .
. .
.


