Обучение нейронной сети
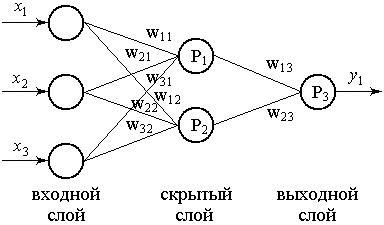
Обучение нейронных сетей является одной из основных областей применения генетических алгоритмов. Для построения и обучения сети создается набор примеров, который представляет собой совокупность векторов вида (X, Y), где X =(x 1, x 2,…, x n) – значения всех входов нейронной сети, а Y =(y 1, y 2,…, y m) – значения всех выходов нейронной сети, которые должны получаться в процессе ее работы. Структура эталонных векторов задает одновременно количество входных и выходных нейронов (в данном случае m и n, соответственно). Целью обучения нейронной сети является достижение такой ситуации, когда при подаче на вход сети любого вектора X из набора примеров на ее выходе получается выходной вектор Y¢, отличающийся от эталонного вектора Y не более чем на заданную заранее величину d. Основными характеристиками нейронной сети являются: · количество скрытых слоев; · количество нейронов в каждом из скрытых слоев; · веса входов каждого из скрытых и выходных нейронов w ij; · функция активации F для каждого скрытого и выходного нейрона. Таким образом, можно обобщенно сформулировать оптимизационную задачу обучения нейронной сети. Исходными данными для нее будут: · количество входных и выходных нейронов; · набор обучающих примеров. В результате решения этой задачи нужно получить следующие значения: · количество скрытых слоев; · количество нейронов в каждом скрытом слое; · значения весов входов для каждого скрытого и выходного нейрона; · функции активации для каждого скрытого и выходного нейрона. Очевидно, что целевой функцией в данном случае будет максимальное отличие выходного вектора Y¢ от эталонного Таким образом, задача обучения нейронной сети сводится к задаче поиска оптимального решения. Заметим, что даже для простейших нейронных сетей эта задача является многомерной и крайне сложной. С другой стороны, цель найти сеть, удовлетворяющую условию Однако, для обучения нейронных сетей генетические алгоритмы в чистом виде, как правило, не применяют. Они обычно используются на различных этапах построения и обучения в качестве основного или вспомогательного инструмента. В частности, генетический алгоритм может использоваться для поиска количества скрытых слоев, нейронов в каждом слое, а также всех значений весов сети и функций активации. Причем функции активации, как правило, выбираются из ограниченного набора, а еще чаще подбирается не сама формула функции активации, а один или несколько ее параметров. В основном генетические алгоритмы используются для улучшения сетей, уже созданных и обученных с помощью какого-либо другого алгоритма. Для иллюстрации применения генетических алгоритмов в области создания и обучения нейронных сетей рассмотрим следующий пример. Пусть имеется нейронная сеть, представленная на рисунке 7.3.
- Рис. 7.3. Пример нейронной сети Сеть состоит из 6 нейронов: трех входных, двух скрытых и одного выходного. Таким образом, сеть имеет всего один скрытый слой нейронов. В качестве функции активации всех скрытых и выходного нейронов используется сигмоидальная функция:
где п – количество входов нейрона, x i – значение на i-м входе, w i – вес i -го входа, а Р –параметр функции активации, влияющий на ее крутизну. Таким образом, вектора примеров будут иметь вид (x 1, х 2, х 3, y 1), где x i – входные значения, а y 1 – эталонное выходное значение. Для вычисления значения целевой функции будем использовать следующую формулу:
где k – количество примеров, Таким образом, целевая функция будет представлять собой максимальное для набора примеров относительное отклонение от эталонного значения, выраженное в процентах. Чем меньше значение целевой функции, тем сеть лучше. Здесь уже можно задать критерий останова генетического алгоритма. Можно указать число поколений, а можно задать условие на значение целевой функции. Например, остановить работу алгоритма, когда для одной из особей значение целевой функции будет равно 5%, что является достаточно хорошим результатом. При обучении нейронных сетей размер популяции выбирается достаточно большим, как минимум 100 особей. Хромосома в данном случае будет представлять массив из 11 действительных чисел, по четыре на каждый скрытый нейрон и три для выходного нейрона, которые представляют собой веса соответствующих входов нейронов и параметры их функций активации:
Для элементов хромосомы – генов – введем ограничения, обусловленные природой нейронных сетей: -1£ w ij£1 и P i>0. В качестве операторов скрещивания, отбора и редукции выберем традиционные операторы, рассмотренные выше при решении задачи нахождения максимума одномерной функции. Для оператора скрещивания можно установить вероятность применения 0,95. В качестве оператора мутации будем использовать случайное изменение значений весов и параметра функции активации для каждого нейрона на случайную величину. Вероятность мутации 0,01. Причем одновременно будет изменяться параметр функции только для одного нейрона и для каждого нейрона будет изменяться один из входных весов. Какие конкретно веса и параметры будут меняться, определяется по равномерному закону. Например, мутация может быть следующей: значение Р2 увеличивается на 0,1; значение w 31уменьшается на 0,05; w 12 – уменьшается на 0,01; vv13 – увеличивается на 0,05. Исходная популяция будет формироваться на основе равномерного распределения для каждого элемента хромосомы. Целью работы генетического алгоритма будет поиск значений весов для всех скрытых и выходных нейронов, а также параметра Р их функций активации. После останова работы такого алгоритма получим обученную нейронную сеть, удовлетворяющую заданным требованиям. Заметим, что в данном примере алгоритм применялся только для построения весовой матрицы сети и вычисления параметров функций активации. Задача полного построения нейронной сети обычно решается в два этапа, на каждом из которых используется свой генетический алгоритм. На первом этапе генетический алгоритм используется для вычисления базовых характеристик: числа скрытых слоев и числа нейронов в каждом скрытом слое. При этом для оценки качества каждого решения используется следующий подход. Нейронная сеть, закодированная в проверяемой особи, обучается в течение фиксированного ограниченного промежутка времени. Обучение может происходить как средствами специального генетического алгоритма, так и другими. Если используется генетический алгоритм, то время обучения может оцениваться количеством поколений. Например, каждая сеть обучается в течение 100 поколений. Затем выбирается лучшая особь, качество которой и определяет качество решения по базовым характеристикам сети. На втором этапе генетический алгоритм используется для вычисления матрицы весов и определения функций активации так, как это было рассмотрено выше. На обоих этапах используется один и тот же набор обучающих примеров, являющийся единственной информацией, использующейся в качестве исходных данных для построения и обучения нейронной сети при решении конкретной задачи. Рассмотренный процесс показывает, насколько сложной является задача построения и обучения нейронной сети как с точки зрения ее размерности, так и с точки зрения ее вычислительной сложности. Тем не менее, генетические алгоритмы предоставляют один из эффективных и изящных путей ее решения. В заключении отметим, что генетические алгоритмы представляют собой подход к решению задачи поиска лучшего решения, а не четко определенный алгоритм. Для решения конкретной задачи, помимо ее формализации, формулировки генотипа и фенотипа, требуется создавать и конкретный генетический алгоритм. Для этого задают значения размера популяции, вероятности мутации и скрещивания, описывают процесс работы операторов отбора, скрещивания, мутации и редукции, что и было показано в рассмотренных примерах. И может оказаться, что алгоритм, успешно решающий одну задачу, совершенно не подходит для решения другой. В настоящее время существует отдельная область исследований, целью которых является создание генетических алгоритмов, эффективно решающих как можно большее число задач.
|

 , полученное среди всех входных векторов. Подбирая значения параметров нейронной сети, можно найти требуемое значение
, полученное среди всех входных векторов. Подбирая значения параметров нейронной сети, можно найти требуемое значение 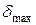 .
.
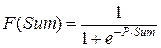 ,
, 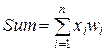 ,
, ,
,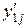 – значение выхода нейронной сети для j -го примера,
– значение выхода нейронной сети для j -го примера, 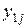 – эталонное значение выхода нейронной сети для j -го примера.
– эталонное значение выхода нейронной сети для j -го примера.


