ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
Уклон – величина наклона одной прямой линии относительно другой, т.е. представляет собой тангенс угла между ними (рис. 1): tgα =
Р и с. 1
Уклон указывают непосредственно у изображения поверхности или на полке линии-выноски в виде соотношения (1:5), в процентах (10 %) или в промилле (5 ‰). Перед размерным числом, определяющим уклон, наносят знак (
Р и с. 2
Конусность – отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними (рис. 3, а):
К
Пред размерным числом, характеризующим конусность, наносят знак (
б в Р и с. 3
Р и с. 4
Построение конусности при заданной длине L и диаметре D одного из оснований можно выполнить графически следующим образом: построить на заданной оси вспомогательный полный конус, у которого произвольно взятое основание а укладывается в высоте столько раз, сколько задано в обозначении конуса. Затем провести образующие искомого конуса параллельно образующим вспомогательного конуса через концы заданного диаметра D, как показано на рис. 4. Сопряжение – плавный переход одной линии в другую. Для построения сопряжений надо знать величину радиуса сопряжений, найти центр, из которого проводят дугу, т.е. центр сопряжений. Затем нужно найти точки, в которых одна линия переходит в другую, т.е. точки сопряжений. Одновременно следует помнить, что без точного построения центра и точек сопряжения невозможно правильно выполнить и обвести чертеж. Точка сопряжения дуги окружности и прямой линии лежит на перпендикуляре, опущенном из центра дуги на сопрягаемую прямую (рис. 5, а), или на линии, соединяющей центры сопрягаемых дуг (рис. 5, б). Ниже приведены примеры построения следующих сопряжений. 1. Сопряжение двух пересекающихся прямых дугой заданного радиуса (рис. 6).
а б
Р и с. 5
Даны пересекающиеся под произвольным углом прямые линии. Нужно построить сопряжения этих прямых дугой заданного радиуса R. Для построения необходимо сделать следующее. 1.1. Найти точку O – центр сопряжения, который должен лежать на расстоянии R от сторон угла, т.е. в точке пересечения прямых, проходящих параллельно сторонам угла на расстоянии R от них. Для проведения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R, сделать засечки и к ним провести касательные. 1.2. Найти точки сопряжений. Для этого из точки O опустить перпендикуляры на заданные прямые. 1.3. Из точки O, как из центра, описать дугу заданного радиуса R между точками сопряжений. 2. Сопряжение двух параллельных прямых (рис. 7). Заданы две параллельные прямые и на одной из них точка сопряжения М.
Р и с. 6
Построение выполняют следующим образом. 2.1. Находят центр сопряжения и радиус дуги. Для этого из точки М восстанавливают перпендикуляр до пересечения с прямой в точке N. Отрезок MN делят пополам. 2.2. Из точки O – центра сопряжения радиусом OM=ON – описывают дугу от точек сопряжения M и N.
а б
Р и с. 7
3. Сопряжение дуги и прямой дугой заданного радиуса (рис. 8). Даны дуга окружности радиуса R и прямая. Требуется соединить их дугой радиуса R 1. 3.1. Находят центр сопряжения, который должен находиться на расстоянии R 1от дуги и от прямой. Поэтому проводят вспомогательную прямую, параллельную заданной прямой, на расстоянии, равном радиусу сопрягающей дуги R 1. Раствором циркуля, равным сумме заданных радиусов R+R 1, описывают из центра О дугу до пересечения с вспомогательной прямой. Полученная точка О 1 – центр сопряжения. 3.2. По общему правилу находят точки сопряжения: соединяют прямой центры сопрягаемых дуг О 1и О, и опускают из центра сопряжения О 1перпендикуляр на заданную прямую. 3.3. Из центра сопряжения О 1между точками сопряжения M и N проводят дугу, радиус которой R 1.
Р и с. 8
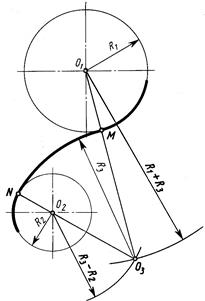
4. Сопряжение двух дуг дугой заданного радиуса (рис. 9). Даны две дуги, радиусы которых R 1и R 2. Требуется построить сопряжение дугой, радиус которой задан. Различают три случая касания: внешнее (рис. 9, а), внутреннее (рис. 9, б) и смешанное (рис. 9, в). 4.1. Для внешнего касания.
а б
в
Р и с. 9 4.1.1. Из центров О 1и О 2 раствором циркуля, равным сумме радиусов заданной и сопрягающей дуг, проводят вспомогательные дуги; радиус дуги, проведенной из центра О 1, равен R 1 +R 3; а радиус дуги, проведенной из центра О 2, равен R 2 +R 3. На пересечении вспомогательных дуг расположен центр сопряжения – точка О 3. 4.1.2. Соединив прямыми точку О 1с точкой О 3и точку О 2с О 3находят точки сопряжения M и N; 4.1.3. Из точки О 3раствором циркуля, равным R 3, между точками M и N описывают сопрягающую дугу. 4.2. Для внутреннего касания выполняют те же построения, но радиусы дуг берут равными разности радиусов заданной и сопрягающей дуг, т.е. R 4- R 1и R 4 – R 2. Точки сопряжения Ри Клежат на продолжении линий, соединяющих точку О4с точками О 1 и О 2. 4.3. Для смешанного (внешнего и внутреннего) касания. 4.3.1. Из центра О1проводят вспомогательную дугу радиусом, равным сумме радиусов сопрягаемой дуги радиуса R 1и сопрягающей дуги радиуса R 3, а из центра О 2проводят вторую вспомогательную дугу радиусом, равным разности радиусов R 3и R 2, до пересечения с первой вспомогательной дугой в точке О 3, которая будет искомым центром сопрягающей дуги. Точки сопряжения находят по общему правилу, соединяя прямыми центры дуг О 3 и О 1; О3и О2. 4.3.2. На пересечении этих прямых с дугами соответствующих окружностей находят точки M и N. Деление окружности на равные части. Наиболее рационально деление окружности на любое число равных частей с помощью таблицы хорд (коэффициентов для деления окружности). Длину (l) хорды, которую откладывают на заданной окружности, определяют по формуле
где l – длина хорды, k - коэффициент, определяемый по таблице 1, d – диаметр заданной окружности. Таблица хорд (коэффициентов для деления окружности)
Циркульные кривые. К ним, в частности, относится овал – замкнутая выпуклая плоская кривая, состоящая из дуг окружности. Построение овала выполняется дугами окружностей из центров О 1, О 2, О 3, и О 4 (рис. 10). Для нахождения центров О 1, О 2 необходимо сделать следующее: 1) отложить на малой оси отрезок ОЕ=ОА, т.е. длину большой полуоси; 2)провести прямую АС, отложив на ней от точки С отрезок СF=СЕ; 3) восстановить перпендикуляр из середины отрезка АF; 4) отметить положение центров О1 и О 2 на пересечении перпендикуляра с заданными осями овала. Два других центра О 3, и О 4 симметричны О 1и О 2 относительно точки О пересечения осей овала; 5) провести из центров О1и О 3 дуги окружностей радиусом R2; 6) провести из центров О 2и О 4 дуги окружностей радиусом R 1.
Р и с. 10
|

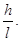

 ), острый угол которого направлен в сторону уклона. Для построения уклона через заданную точку нужно построить прямоугольный треугольник с одной из вершин в заданной точке К, так как это показано на рис. 2. Отношение катетов должно соответствовать отношению, указанному в обозначении уклона.
), острый угол которого направлен в сторону уклона. Для построения уклона через заданную точку нужно построить прямоугольный треугольник с одной из вершин в заданной точке К, так как это показано на рис. 2. Отношение катетов должно соответствовать отношению, указанному в обозначении уклона.

 ), острый угол которого должен быть направлен в сторону вершины конуса. Обозначение конуса может быть проставлено над осью (рис. 3, б) или на полке линии-выноски (рис. 3, в).
), острый угол которого должен быть направлен в сторону вершины конуса. Обозначение конуса может быть проставлено над осью (рис. 3, б) или на полке линии-выноски (рис. 3, в).

 а
а