Лекальные кривые. К лекальным кривым относятся эллипс, синусоида и др.
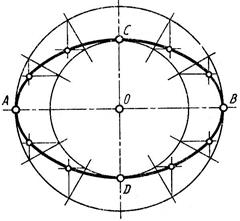
Эллипс – замкнутая выпуклая плоская кривая, сумма расстояний от любой точки которой до двух данных точек (фокусов) всегда равна длине большой оси эллипса (рис. 11).
Р и с. 11
Размеры эллипса определяются величинами его большой АВ и малой CD осей. В начале построения описывают две концентрические окружности диаметром AB и CD. Затем большую окружность делят на равные части, например 12. Точки деления соединяют прямыми, проходящими через центр окружностей. Из точек пересечения прямых с окружностями проводят линии, параллельные осям эллипса. При взаимном пересечении этих линий получают точки, принадлежащие эллипсу.
Точки пересечения одноименных вспомогательных прямых и принадлежат синусоиде.
Р и с. 12
Для обводки кривой по лекалу рекомендуется соединить полученные точки тонкой линией от руки на глаз, стараясь при этом придать кривой линии возможно более плавные очертания, и лишь после этого подобрать лекало, соответствующее кривизне того или иного ее участка, соединяя не менее трех-четырех точек одновременно (рис. 13).
Р и с. 13
|
Синусоида – плоская кривая, изображающая изменения синуса в зависимости от изменения его аргумента – угла α (рис. 12). При построении синусоиды данную окружность делят на произвольное количество равных частей. На продолжении горизонтального диаметра окружности по оси х откладывают отрезок АА 1 = 2π R, разделив его на то же количество равных частей. Через точки деления окружности необходимо провести ряд прямых, параллельных АА 1; из точек деления прямой АА1– ряд прямых, перпендикулярных АА 1.
