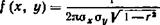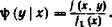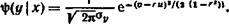Рассмотрим двумерную случайную величину
(X, Y). Если обе функции регрессии Y на X и X на Y линейны (см. § 15), то говорят, что X и К связаны линейной корреляционной зависимостью. Очевидно, что графики линейных функций регрессии — прямые линии, причем можно доказать, что они совпадают с прямыми среднеквадратической регрессии (см. § 20). Имеет место следующая важная теорема. Теорема. Если двумерная случайная величина (X, Y) распределена нормально, то X и Y связаны линейной корреляционной зависимостью. Доказательство. Двумерная плотность вероятности (см. § 19)
Где и = (х —аг)/а*, v = {у —а,)/о,. Плотность вероятности составляющей X (см. § 19, замечание) Найдем функцию регрессии М (У |х), для чего сначала найдем условный закон распределения величины Y при Х—х [см. § 14, формула (**)]:
Подставив (*) и (**) в правую часть этой формулы и выполнив выкладки, имеем
Заменив и и v по формулам (**), окончательно получим
Полученное условное распределение нормально с математическим ожиданием (функцией регрессии Y на X) M{Y\x) = a9+r ^{x—aj UJC и дисперсией aj(l— г3). Аналогично можно получить функцию регрессии X на Y : М(Х\у) = а1 + г^-(у—аг). Так как обе функции регрессии линейны, то корреляция между величинами X и Y линейная, что и требовалось доказать. Принимая во внимание вероятностный смысл параметров двумерного нормального распределения (см. § 19), заключаем, что уравнения прямых регрессии У—а, = г-^-(дс—at), x—at = г %*-(у—а%) совпадают с уравнениями прямых среднеквадратической регрессии (см. § 20). Задачи
|