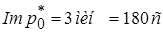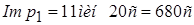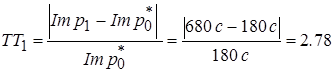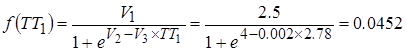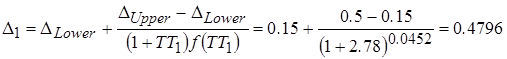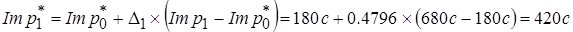Описание Технологического процесса. Иллюстрация 16: Назначение при изучающем методе
Иллюстрация 16: Назначение при изучающем методе
Пример
| Номер связи
| Тип
| Длина (м)
| v0 (км/ч)
| Пропускная способность (авт/ч)
| Imp0* (мин)
| |
|
|
|
|
| 03:00
| |
|
|
|
|
| 03:00
| |
|
|
|
|
| 03:00
| |
|
|
|
|
| 03:00
| |
|
|
|
|
| 03:00
| |
|
|
|
|
| 03:00
| |
|
|
|
|
| 12:00
| |
|
|
|
|
| 03:45
| |
|
|
|
|
| 10:00
| |
|
|
|
|
| 05:00
| | Маршрут
| Связи
| Длина
|
|
| Imp0*
| |
| 1+8+9
|
|
|
| 0:18:45
| |
| 1+2+3+5+6+7
|
|
|
| 0:18:00
| |
| 10+11+5+6+7
|
|
|
| 0:24:00
| | Ввести параметры:
· BPR функция с a = 1, b = 2, c = 1
· ΔLower = 0.15
· ΔUpper = 0.5
· V1 = 2.5
· V2 = 4
· V3 = 0.002
|
Иллюстрация 17: Импеданс незагруженной сети, при входных (с введением) параметрах изучающего метода.
| Номер связи
| Интенсивность 1
(авт/ч)
| Imp 1
(мин)
| TT1
| F(TT1)
| Δ1
| Imp*1 (мин)
| |
|
| 11:20
| 2,78
| 0,0452
| 0,4796
| 07:00
| |
|
| 11:20
| 2,78
| 0,0452
| 0,4796
| 07:00
| |
|
| 11:20
| 2,78
| 0,0452
| 0,4796
| 07:00
| |
|
| 11:20
| 2,78
| 0,0452
| 0,4796
| 07:00
| |
|
| 11:20
| 2,78
| 0,0452
| 0,4796
| 07:00
| |
|
| 11:20
| 2,78
| 0,0452
| 0,4796
| 07:00
| |
|
| 12:00
| 0,00
| 0,0450
| 0,5000
| 12:00
| |
|
| 03:45
| 0,00
| 0,0450
| 0,5000
| 03:45
| |
|
| 10:00
| 0,00
| 0,0450
| 0,5000
| 10:00
| |
|
| 05:00
| 0,00
| 0,0450
| 0,5000
| 05:00
| | Маршрут
| Интенсивность 1
| Imp 1
|
|
|
| Imp*1
| |
|
| 0:27:05
|
|
|
| 0:22:45
| |
|
| 1:08:00
|
|
|
| 0:41:59
| |
|
| 0:49:00
|
|
|
| 0:35:59
| Иллюстрация 18: Пример изучающего метода: 1 шаг итерации
| Номер связи
| Интенсивность 2
(авт/ч)
| Imp 2
(мин)
| TT2
| F(TT2)
| Δ2
| Imp*2 (мин)
| |
|
| 11:20
| 0,62
| 0,0450
| 0,4925
| 09:08
| |
|
| 05:05
| 0,27
| 0,0450
| 0,4962
| 06:03
| |
|
| 05:05
| 0,27
| 0,0450
| 0,4962
| 06:03
| |
|
| 05:05
| 0,27
| 0,0450
| 0,4962
| 06:03
| |
|
| 05:05
| 0,27
| 0,0450
| 0,4962
| 06:03
| |
|
| 05:05
| 0,27
| 0,0450
| 0,4962
| 06:03
| |
|
| 30:45
| 1,56
| 0,0451
| 0,4855
| 21:06
| |
|
| 09:37
| 1,56
| 0,0451
| 0,4855
| 06:36
| |
|
| 10:00
| 0,00
| 0,0450
| 0,5000
| 10:00
| |
|
| 05:00
| 0,00
| 0,0450
| 0,5000
| 05:00
| | Маршрут
| Интенсивность 2
| Imp 2
|
|
|
| Imp*2
| |
|
| 0:51:42
|
|
|
| 0:36:50
| |
|
| 0:36:45
|
|
|
| 0:39:22
| |
|
| 0:30:15
|
|
|
| 0:33:08
|
Иллюстрация 19: Пример изучающего метода: 2 шаг итерации
| Номер связи
| Интенсивность 3
(авт/ч)
| Imp 3
(мин)
| TT3
| F(TT3)
| Δ3
| Imp*3 (мин)
| |
|
| 06:42
| 0,27
| 0,0450
| 0,4963
| 07:56
| |
|
| 03:56
| 0,35
| 0,0450
| 0,4953
| 05:00
| |
|
| 03:56
| 0,35
| 0,0450
| 0,4953
| 05:00
| |
|
| 06:42
| 0,11
| 0,0450
| 0,4984
| 06:22
| |
|
| 06:42
| 0,11
| 0,0450
| 0,4984
| 06:22
| |
|
| 06:42
| 0,11
| 0,0450
| 0,4984
| 06:22
| |
|
| 20:20
| 0,04
| 0,0450
| 0,4994
| 20:43
| |
|
| 06:21
| 0,04
| 0,0450
| 0,4994
| 06:28
| |
|
| 27:47
| 1,78
| 0,0451
| 0,4842
| 18:37
| |
|
| 13:53
| 1,78
| 0,0451
| 0,4842
| 09:18
| | Маршрут
| Интенсивность 3
| Imp 3
|
|
|
| Imp*3
| |
|
| 0:33:23
|
|
|
| 0:35:07
| |
|
| 0:34:40
|
|
|
| 0:37:03
| |
|
| 1:01:47
|
|
|
| 0:47:02
|
Иллюстрация 20: Пример изучающего метода: 3 шаг итерации
Иллюстрации с33 по 36 иллюстрируют первые три итеративных шага процедуры изучения на примере сети:
1 шаг итерации, n = 1
• Интенсивность 1: интенсивность, следующая из результатов итеративного шага 1 "все или ничего" назначения на маршрут с самым низким показателем импеданса в разгруженной сети. Для Imp0 * это - маршрут 2, который загружен 2000-ми автомобильных поездок.
• текущий импеданс Imp1: текущий Imp1 следует из результатов для каждой связи от HCM функции пропускной способности (a = 1, b = 2, c = 1). Для связи 1, например, может быть выполнен следующий расчет:
Imp1 (связь 1), = 3 мин.∙(1 + (2000/1200)2) = 11мин 20 с
•Предполагаемый импеданс Imp1*: предполагаемый импеданс Imp1* каждой связи, состоящий из текущего импеданса Imp1 и предполагаемого Imp0* на последнем итеративном шаге. Это следует из коэффициента обучения Δ. Чтобы определить Imp1* для связи 1, необходимы следующие вычисления:
 
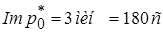
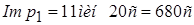
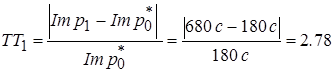
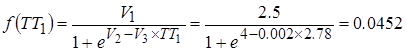
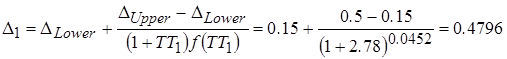
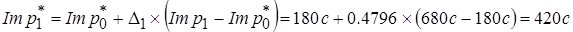
2 шаг итерации, n = 2
• Интенсивность 2: маршрут с самым низким показателем импеданса для Imp1* – маршрут 1. Теперь имеют место два маршрута, – это маршруты 1 и 2. Каждый маршрут загружен с 1/n, то есть, с таким требованием, чтобы каждый маршрут использовался 1000-ей автомобилей.
• Текущий импеданс Imp2: текущий импеданс Imp2 с каждой связи увеличивается на вновь загруженных связях 8 и 9, и уменьшается на связях 2, 3, 5, 6 и 7.
• Предполагаемый импеданс Imp2*: предполагаемый импеданс Imp2* каждой связи состоит из текущего импеданса Imp2 и предполагаемого импеданса Imp1* последнего итеративного шага.
3 шаг итерации, n = 3
• Интенсивность 3: маршрут с самым низким показателем импеданса для Imp1* – это теперь маршрут 3. 1/3 от 2000 автомобильных поездок теперь распределена по маршрутам 1, 2 и 3.
• Текущий импеданс Imp3: текущий импеданс Imp3 снова следует из текущей интенсивности 3 посредством CR-функции.
• Предполагаемый импеданс Imp*: предполагаемый импеданс Imp3* каждой связи состоит из текущего импеданса Imp3 и предполагаемого Imp2* последнего итеративного шага.
4 шаг итерации, n = 4
Закончившийся поиск маршрута, основанный на Imp3*, определяет маршрут 1 как самый короткий маршрут. Таким образом, результат интенсивности следующих маршрутов:
• интенсивность маршрута 1 = 2/4 • 2000 = 1000 поездок
• интенсивность маршрута 2 = 1/4 • 2000 = 500 поездок
• интенсивность маршрута 3 = 1/4 • 2000 = 500 поездок
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|
|
Анализ микросреды предприятия Анализ микросреды направлен на анализ состояния тех составляющих внешней среды, с которыми предприятие находится в непосредственном взаимодействии...
Типы конфликтных личностей (Дж. Скотт) Дж. Г. Скотт опирается на типологию Р. М. Брансом, но дополняет её. Они убеждены в своей абсолютной правоте и хотят, чтобы...
Гносеологический оптимизм, скептицизм, агностицизм.разновидности агностицизма Позицию Агностицизм защищает и критический реализм. Один из главных представителей этого направления...
|
|
ЛЕКАРСТВЕННЫЕ ФОРМЫ ДЛЯ ИНЪЕКЦИЙ К лекарственным формам для инъекций относятся водные, спиртовые и масляные растворы, суспензии, эмульсии, новогаленовые препараты, жидкие органопрепараты и жидкие экстракты, а также порошки и таблетки для имплантации...
Тема 5. Организационная структура управления гостиницей 1. Виды организационно – управленческих структур. 2. Организационно – управленческая структура современного ТГК...
Методы прогнозирования национальной экономики, их особенности, классификация В настоящее время по оценке специалистов насчитывается свыше 150 различных методов прогнозирования, но на практике, в качестве основных используется около 20 методов...
|
|
