Некоторые свойства проекций точек, линий и плоскостей

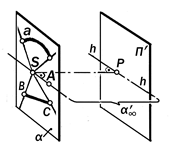
Так как вариантов взаимного рас-положения изображаемых элементов пространства по отношению к центру проецирования и картине бесчислен-ное множество, то для описания свой-ств их проекций из этого множества рассмотрим наиболее характерные час-

тные случаи.

Случай 1. Изображаемая прямая а проходит через центр проецирования S и не параллельна картине П ¢ (рис. 6.4): а ' S Ù a ∦ П¢;.

С л е д с т в и е:

а ' S Ù a ∦ П ¢ Þ a¢; = a ´ П¢ - точка.

Если изображаемая прямая а про-ходит через центр S проецирования и не параллельна картине П ¢, то её про-екцией будет точка а ¢, с которой совпа-дут проекции А¢, В¢;,…всех точек А,В,…, принадлежащих прямой а. При этом го-ворят, что прямая а «выродилась» в точку, на которой «собрались» проек-ции всех принадлежащих ей точек.

Другими словами, коллинейные то-чки А,В, …проецирующей прямой в ре-зультате их проецирования преобра - зовались в их тождественные проек-ции А ¢,В¢,…, инцидентные вырожден-ной проекции а¢; прямой а.

Определение 6.7. Тождественное расположение проекций коллинейных точек проецирующей прямой опреде-ляет с о б и р а т е л ь н о е свойство её вырожденной проекции.

Утверждение 6.5. При заданном аппарате проецирования (S, П¢) одна проекция изображаемой точки не опре-деляет положения этой точки в про-странстве, так как с этой проекцией совпадает одно параметрическое мно-

жество проекций всех остальных то-

чек проецирующего луча.

Случай 2. Изображаемая прямая а проходит через центр S и параллельна картине П ¢ (рис.6.5):

а ' S Ù a || П;

Рис. 6.6. Собирательное свойство

вырожденной проекции плоскости

Рис. 6.7. Нейтральная плоскость

Рис. 6.8. Элементы, принадлежащие картине, совпадают со своими проекциями и выглядят в натуральную величину

Рис.6.9. Вершина конуса совпадает с центром проецирования

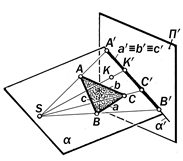
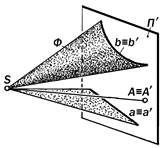
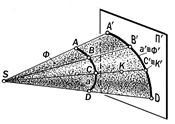
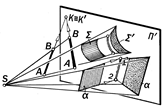
Рис6.10 Элементы пространства не параллельны картине, а поэтому её пересекают

С л е д с т в и е: Так как прямая а па-

раллельна картине П ¢, то она её н е

п е р е с е к а е т и поэтому на картине н е и з о б р а ж а е т с я. Если до-пустить, что прямая а пересекает кар-тину П ¢ в бесконечности, тогда её вы-рожденная проекция а ¢_¥ в виде точки будет её б е с к о н е ч н о– у д а л ё н- н о й или н е с о б с т в е н н о й точкой.

Случай 3. Изображаемая плоскость

a проходит через центр проецирования S и не параллельна картине П ¢ (рис.6.6).

a ' S Ù a ∦ П¢;.

С л е д с т в и е. Так как изображаемая плоскость a проходит через центр S и не параллельна картине П ¢, то она, яв-ляясь проецирующей, проецируется на картину в прямую a¢, с которой сов-падают проекции А ¢,…, а ¢,… всех при-надлежащих ей точек и линий.

Другими словами, компланарные точки А, В,… и линии а, b,…проецирую-щей плоскости a преобразуется в их тождественные проекции А ¢ º а ¢ º b ¢, инцидентные вырожденной проекции a¢; плоскости a.

Определение 6.8. Тождественное расположение проекций компланарных точек и линий проецирующей плоско-сти определяет с о б и р а т е л ь -

н о е свойство её вырожденной проек-ции.

Случай 4. Изображаемая плоскость a проходит через центр S и параллель-на картине П ¢ (рис.6.7):

a ' S Ù a || П¢;.

С л е д с т в и е. Если проецирующаяплоскость a параллельна картине П¢;,

то её картинный след a¢_¥ бесконечно удалён и практически не изображается. Это значит, что невозможно изобразить

какие бы то ни было инциденции этой плоскости, т.е., её точки и линии.

Определение 6.9. Плоскость, про-ходящая через центр проецирования и параллельная картине, называется н е й т р а л ь н о й.

Случай 5. Изображаемые точки, прямые и плоские кривые совпадают с плоскостью картины П ¢ (рис 6.8).

А,…,а,…, с,… Î П¢;

С л е д с т в и е:Если картинная плоско-

сть проходит через некоторые точки,

прямые или кривые линии изображае-мого объекта (или пересекает его по этим линиям), то эти точки и линии

с о в п а д а ю т со своими проекциями

и поэтому являются двойными:

А,…, а,…, с,…ÎП ¢; Þ А º А¢, а º а ¢,

с º с ¢.

При этом говорят, что эти точки и линии «изображают самих себя », а по-этому их особым изобразительным сво-йством является то, что на картине они выглядят в «натуральную величину».

Случай 6. Вершина Е изобража-емой конической поверхности совпа-дает с центром проецирования S. (рис.

6.9).

С л е д с т в и е. Если изображаемая коническая поверхность является прое-цирующей, то её картинным следом бу-дет линия Ф ¢ как вырожденная проек-ция поверхности Ф, на которой распо-лагаются проекции всех её точек и ли-ний.

А, К,…, а,.. Î Ф Þ А¢, К¢, а¢,..º Ф¢.

Случай 7 (общий). Изображаемые прямые, плоские фигуры и отсеки по-верхностей не проходят через центр проецирования и не параллельны кар-тине (рис. 6.10.)

С л е д с т в и е. Если изображаемые прямые, плоские фигуры и отсеки по-верхностей не параллельны картине, то они при продолжении её пересекают.

Определение 6.10. Результаты пересечения проецируемых элементов изображаемого объекта с картинной плоскостью называются их к а р-

т и н н ы м и с л е д а м и.

Так как картинные следы принад-лежат и изображаемым элементам, и картинной плоскости, то они являются двойными и сами себя изображают (см. случай 5). Их отличительной пози-ционной особенностью является то, что их вид и положение на картине зависят от вида изображаемого элемента и его расположения по отношению к картине и не зависит от расположения центра проецирования в пространстве. Это означает, что при изменении положе-ния центра в пространстве проекции изображаемых элементов на картин-ной плоскости будут изменять свою форму, а положение и вид их картин-ных следов будут оставаться неизмен-ными.

 

 

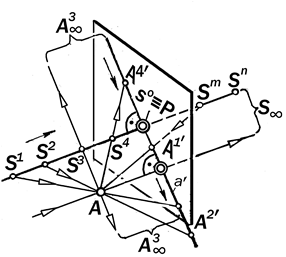
Рис.6.11 Аппарат центрального

подвижного проецирования