Обратимых проекций

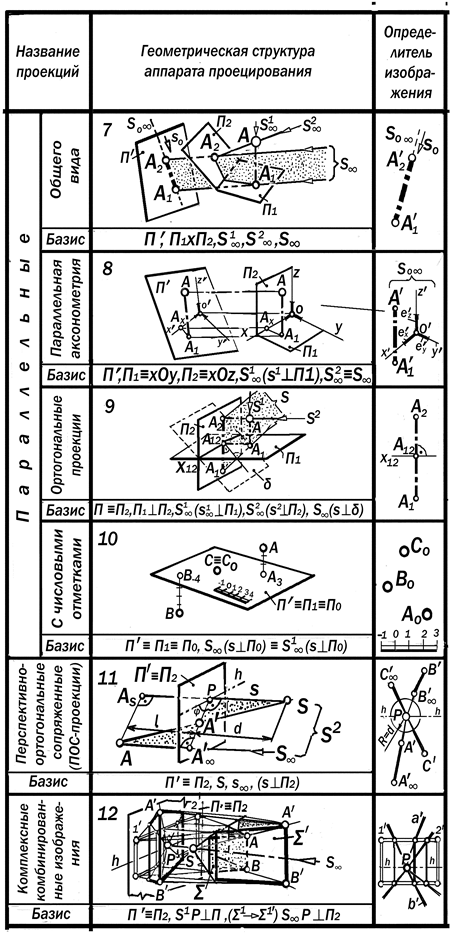
Требование обратимости проекци-онного изображения сформировало концепцию метода двух изображений, лежащего в основе получения проекци-онных чертежей, структура которых изо-морфна структуре изображаемых объ-ектов (рис.6.22).

В общем случае аппарат этого ме-тода состоит из трёх плоскостей П ¢, П ₁

и П ₂ и сопряжённых с ними трёх колли-нейных центров S, S ¹ и S ². Плоскость П ¢ называется основной плоскостью

проекций или к а р т и н о й, а плоскос-ти П ₁ и П ₂ - вспомогательными (рис. 6. 22, п.1).

Для получения обратимого черте-жа точки А её проецируют прежде из центра S ¹ на П ₁ и получают первую первичную проекцию А _1, потом – из центра S ² на П ₂ и получают вторую первичную проекцию А ₂ , а затем полу-

 

 

 

Рис. 6.22. Варианты геометрической

структуры аппарата

метода двух изображений

(начало)

 

 

 

Рис. 6.22 Варианты геометрической структуры аппарата метода двух изображений

(начало)

 

 

Рис.6.22. Варианты геометрической

структуры аппарата метода

двух изображений (окончание)

 

ченные первичные проекции А ₁ и А ₂ из

центра S проецируют на П ¢ и получают пару коллинейных вторичных проекций А ₁¢ и А ₂¢. Прямая, на которой лежат эти проекции, называется л и н и е й с в я-

з и. Она проходит через картинный след S ₀ линии центров, называемый центром соответствия вторичных про-екций А₁ и А ₂.

Определение 6.22. Система двухвзаимосвязанных вторичных проекций объекта называется его д в у х к а р- т и н н ы м к о м п л е к с н ы м

ч е р т е ж о м.

Плоскости П ₁ , П ₂ и П ¢ и сопряжен-ные с ними центры S ¹, S ² и S составля-

ют ф и к с и р о в а н н ы й б а з и саппарата метода двух изображений или его структуру [72]. Различные варианты конструкций фиксированного базиса определяют различные виды проекций, составляющие двухкартин-ные комплексные чертежи (рис. 6.22, п. п. 2 – 12).

Если на взаимное расположение П _1,

П ₂ и П ¢ и собственных центров S ¹, S ², S не налагается никаких условий, то по-лучаемый двухкартинный комплексный чертёж являются ц е н т р а л ь н о й

п р о е к ц и е й общего вида (рис. 6. 22, п.1).

Если система плоскостей проекций

П ₁^ П ₂ отнесена к натуральной системе декартовых координат так, что П ₁ º хОу, П ₂ º xOz, а П ¢ расположена про-извольно, центр S ¹ удалён в бесконеч-ность и ортогонально сопряжен с П _1, а S ²º S, то комплексный чертёж точки А вместе с проекцией на П ¢ проградуиро-ванных осей координат является ц е н -

т р а л ь н о й а к с о н о м е т р и е й (рис.6.22, п. 2).

Если центр S ¹ удалён в бесконеч-ность и ортогонально сопряжен с П₁, а S² º S, то получаемый двухкартинный комплексный чертёж является п е р- с п е к т и в о й н а н а к л о н н о й

к а р т и н е (рис. 6. 22, п. 3).

Если П ₁ горизонтальна, П ₂ ^ П ₁, а П ¢ || П ₂ или П ¢º П ₂, центр S ¹ ортого-нально сопряжен с П ₁, а S ² º S, то по-лучаемый двухкартинный комплексный чертёж является п е р с п е к т и в о й

н а в е р т и к а л ь н о й к а р т и н е.

(рис. 6. 22, п.4).

Если геометро-графически промо-делировать динамизм зрительного вос-приятия, то получим аппарат централь-ного подвижного проецирования (см. определение 6.13), имеющий две мо-дификации – с подвижным центром S при неподвижной картине (рис.6.22,п.5) и с подвижной проекционной системой «центр-картина», (рис.6.22, п.6).

Если П ₁ удалена в бесконечность, П ₂ º П ¢, s ^ П ¢, где s – траектория дви-жения S, а 0 £ SP £ ¥, то на П ¢ получа-ем не двух, а много- или поликартин-ный комплексный чертёж или к и н о-

п е р с п е к т и в у (п. 5).

Если П ₂ º П ¢, а П ¢ движется так, что расстояние от подвижного центра S до П ¢, равное D, остаётся неизменным и траектория s ^ П ¢, то на подвижной кар-тине возникает деформирующееся пер-спективное изображение или киноперс-пектива, а на каждом фиксированном положении картины – отдельная стати-чная перспектива (подобно отдельно-му кадру киноплёнки). Если этим ап-паратом изображать проектируемый объект, то получится его киноперспек- т ивная мультипликация (п.6).

Если П ₁ отсутствует, П ₂ º П ¢, центр S ортогонально сопряжен с П ¢, центр S ² удалён в бесконечность и ортогонально сопряжен с картиной, | SP | = d = const, a

расстояния от изображаемых точек до П ¢ различны, но известны, то получае-мый комплексный чертёж называется

п е р с п е к т и в н о – о р т о г о н а л ь-н ы м с о п р я ж е н и е м (или ПОС –

проекцией, предложенной проф. Н.Л.Ли-

хачёвым [60] (Рис.6.22, п.11)

Если П ₁ отсутствует, П ₂ º П ¢, S ²º S и этот двойной центр является центром пространственного гомологического преобразования изображаемого объек-та S в гомологичный ему объект S¹ при плоскости картины как двойной плоско-сти гомологии, то результат проециро-вания полученной в пространстве связ-ной фигуры как системы двух объектов

(см. также рис. 6.20) на картину П ¢ явля-

ется обратимым к о м п л е к с н ы м

к о м б и н и р о в а н н ы м и з о б р а-

ж е н и е м, предложенным профес-сором И.И.Котовым [53],(рис.6.22, п.12).

При помощи перечисленных аппа-ратов центрального проецирования

 

строятся перспективные чертежи про-ектируемых объектов, широко приме-няемых в архитектурном и дизайнер-

ском проектировании.

Определение 6.23. Перспектив-ные чертежи, получаемые аппарата-ми центрального проецирования, фик-сированный базис которых состоит из плоскостей и центров-точек, а про-ецирование осущетвляется прямоли-нейными лучами, называются л и н е й-

н ы м и.

Линейные перспективы являются

традиционными и классическими вида-ми наглядных изображений. Если же идти по пути обобщений с целью полу-чения новых видов перспективных изо-бражений, то в фиксированном базисе аппарата центрального проецирования необходимо менять линейные элемен-ты на нелинейные. К примеру, вместо плоской картины принимать цилиндри-ческую, коническую или сферическую, заменять точку-центр на обобщенный центр в виде определённой поверхнос-ти, а вместо прямолинейных применять ломаные или криволинейные лучи. Тог-

да получаемые перспективные изобра-жения будут н е л и н е й н ы м и геометро-графическими моделями изо-бражаемого объекта, изучение изобра-зительных свойств которых является предметом исследования системной на-чертательной геометрии как фундаме-нтальной науки.

Если все центры проецирования удалены в бесконечность, а плоскости П ₁, П ₂ и П ¢ фиксированного базиса расположены в пространстве произво-льно, то изображениями, составляю-щими двухкартинный комплексный чер-тёж, будут п а р а л л е л ь н ы е п р о- е к ц и и (рис. 6.22, п.7).

Если все три центра удалены в бес-конечность, а плоскости П ₁, и П ₂ сов-падают с координатными плоскостями трёх проградуированных осей декарто-вых координат Охуz, к которым в прост-ранстве отнесена точка А, то её двух-картинный комплексный чертёж вместе с изображением системы координат-ных осей является п а р а л л е л ь --

н о й а к с о н о м е т р и е й (рис.6. 22, п.8).

Если П ₁ горизонтальна, П ₂ ^ П ₁ и

П ¢ º П ₂, центры S ¹ и S ² ортогонально сопряжены с П ₁ и П ₂, а центр S орто-гонально сопряжен с биссекторной пло-скостью d, то изображениями, соста-

вляющими получаемый двухкартинный комплексный чертёж, будут о р т о г о -

н а л ь н ы еп р о е к ц и и(рис.6.22, п.9).

Если не использовать П ₂ и S ², П ₁ со-вместить с П¢ и расположить горизон-тально, ортогонально сопряженные с ними центры S ¹ и S удалить в беско-нечность, а получаемые проецирова-нием из них проекции точек сопровож-дать числами, указывающими на удале-ние в единицах линейного масштаба изображаемых точек от этой плоскости, то изображениями, составляющими по-лученный двухкартинный комплексный чертёж, будут п р о е к ц и и с ч и сл о- в ы м и о т м е т к а м и (рис. 6.22, п.10), [72].

Общим для всех рассмотренных аппаратов центрального и параллель-ного проецирования является то, что

получаемые с их помощью проекции прямолинейных элементов пространст-ва в общем случае также прямоли-нейны. Это обеспечивает наглядность и возможную измеримость чертежа.

Теорема Егера. Если принять,что

проекция прямой линии в общем случае

представляет собой прямую линию, то проецирующие линии образуют

связку прямых и задают центральное или параллельное проецирование.

[ 54].

Из теоремы Егера следует, что свойства сохранения прямолинейности присущи лишь тем аппаратам проеци-рования, в которых проецирующие ли-нии образуют связку прямых.