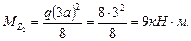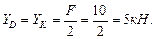Введение 3 страница
Рассмотрим равновесие подвесной балки СЕ. Определим реакции опор. Реакцию YE прикладываем к балке с обратным знаком.
Рис.4.7. Схема шарнирной балки и эпюры поперечных сил и изгибающих моментов.
Проверяем правильность определения реакций опор:
Cтроим эпюры поперечных сил и изгибающих моментов на участке CE шарнирной балки: В точке E: В точке D (правее): В точке D (левее): В точке С:
Построим эпюры поперечных сил и изгибающих моментов на консольной балке АС: В точке С: В точке B (правее): В точке B (левее): В точке A:
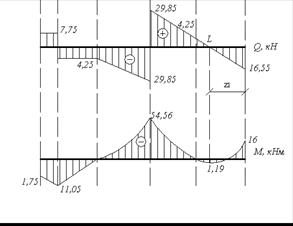
Определим момент в точке L (эпюра поперечных сил меняет знак):
Проверим несущую способность балки:
моментов, рис.4.7),
Прочность балки по нормальным напряжениям обеспечена.
Проверим прочность балки по касательным напряжениям:
Для двутавра №24 из сортамента (Приложение 1):
Прочность балки по касательным напряжениям обеспечена.
З а д а ч а 4.8.
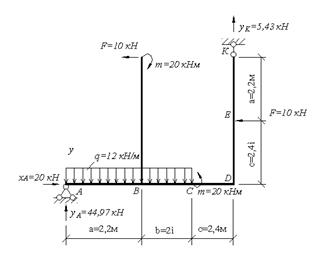
Для заданной рамы (рис 4.8) построить эпюры внутренних усилий, если m=20 кН·м, q=12 кН/м, F=10кН.
Решение. Определим реакции опор, составив уравнение равновесия: ΣМА = 0:
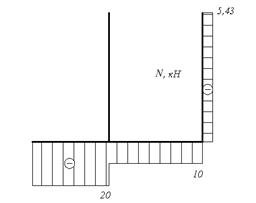
Рис.4.8 Схема рамы и эпюра продольных сил.
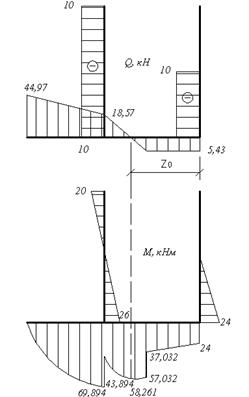
Проверим правильность определения опорных реакций:
Рис.4.9 Эпюры поперечных сил и изгибающих моментов.
Построим эпюру продольных сил (рис.4.8): Участок АВ: Участок BD: Участок KD:
Построим эпюры поперечных сил (рис.4.9): Участок АВ: в точке А: Участок BD: в точке С: Участок ЕD: в точке Е: Участок LB: в точке L: Построим эпюру изгибающих моментов (рис.4.9): Участок АВ:
Участок LВ:
Участок BС:
Участок КD:
Участок DC:
Определим
Задача 4.9.
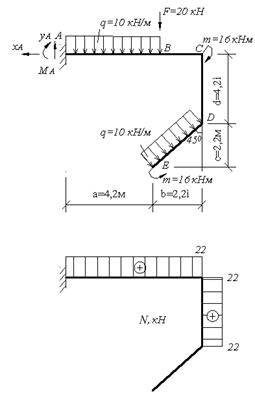
Для заданной рамы (рис 4.10) построить эпюры внутренних усилий, если m=16 кН·м, q=10 кН/м, F=20кН.
Решение. Определим реакции опор:
Построим эпюру продольных сил (рис.4.10): Участок DE: Участок CD:
Участок АС:
Построим эпюры поперечных сил (рис 4.11): Участок DE:
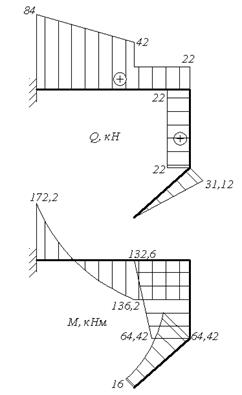
Рис. 4.10. Схема рамы и эпюра продольных сил. Участок CD:
Участок BC:
Участок АВ:
Построим эпюры изгибающих моментов (рис.4.11):
Рис. 4.11. Эпюры поперечных сил и изгибающих моментов. Участок ED:
Участок СD
Участок СВ:
Участок ВА: МВ = 116,6 кН·м, (растянутые волокна снизу).
Задача 4.10 Балка нагружена расчетной нагрузкой. Материал балки – сталь с расчетными сопротивлениями R=210МПа, Требуется: 1) подобрать сечение двутаврового профиля и проверить прочность в учетом собственного веса; 2) в одном из сечений балки, имеющем одновременно большие значения поперечной силы Q и изгибающего момента M, определить напряжения σ и τ на уровне примыкания полки к стенке и проверить прочность используя энергетическую теорию прочности; для сравнения выполнить проверку прочности по третьей теории прочности; выделить вокруг указанной точки элемент балки и показать на схеме нормальные, касательные и главные напряжения; 3) используя один из известных методов определить прогибы посередине пролета и на конце консоли, построить эпюру прогибов балки; 4) проверить жесткость балки при допустимом относительном прогибе:
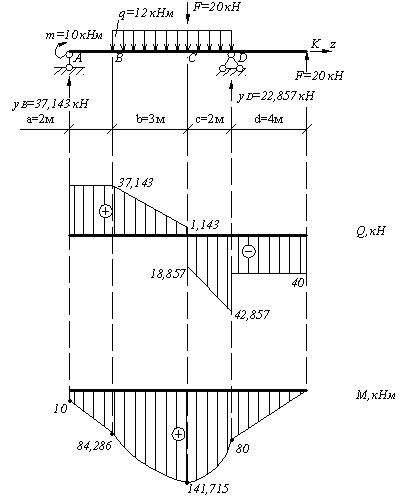
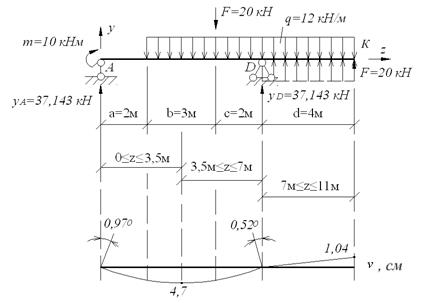
а=2 м, b=3 м, с=2 м, d=4 м, F=20 кН, M=10 кНм, q=12кН/м. Рис. 4.12. Схема балки.
Определим опорные реакции в балке и построим эпюры поперечных сил и изгибающих моментов. Составим уравнение равновесия:
Осуществляем проверку правильности определения опорных реакций:
Рис.4.12. Схема балки. Эпюры поперечных сил и изгибающих моментов
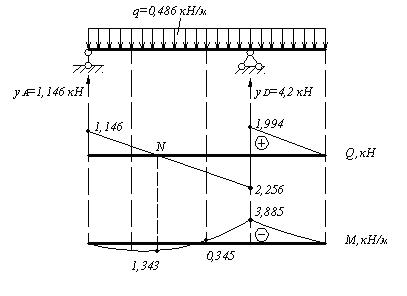
Рис.4.13. Эпюры поперечных сил и изгибающих моментов от собственного веса балки.
Строим эпюру изгибающих моментов (рис 4.13):
Пользуясь сортаментом (Приложение1), выбираем двутавр №36:
Проверим прочность балки с учетом собственного веса. Определим опорные реакции от действия собственного веса балки (q=0,486кН).
Построим эпюры поперечных сил и изгибающих моментов.
Усилия в балке с учетом собственного веса:
Прочность балки с учетом собственного веса:
Прочность балки с учетом собственного веса обеспечена. Проверим прочность балки по главным напряжениям. Выберем опасное сечение балки, в котором имеется сочетание максимального изгибающего момента и поперечной силы. (точка С):
Проведем анализ сечения. Определим нормальные и касательные напряжения в точке 1 (сжатие):
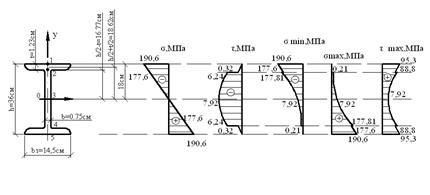
Рис.4.15. Сечение балки. Эпюры нормальных и касательных напряжений.
(статический момент площади сечения выше точки 2).
Определим экстремальные касательные напряжения в точке 2 сечения:
Главные напряжения:
Проведем полную проверку прочности балки, используя энергетическую теорию прочности:
Прочность балки по главным напряжениям обеспечена. Построим эпюры нормальных и касательных напряжений, действующих в поперечном сечении балки (рис 4.15). Рассчитаем главные напряжения, действующие в сечении С.
Для точки 1:
Для точки 2:
Для точки 3.
Для точки 4.
Рассчитаем максимальные касательные напряжения, действующие в сечении:
Для точки 1:
Для точки 2:
Для точки 3:
Построим эпюру максимальных касательных напряжений (рис4.15). Построим упругую линию балки, используя метод начальных параметров. Обобщенное уравнение изогнутой оси имеет вид:
где а, в и с - координаты соответствующих нагрузок.
Рис 4.16. Упругая линия балки. Для определения начальных параметров Запишем уравнение прогибов для Z =7м:
Определим прогиб в середине пролета при Z =3,5м:
Определим прогиб в конце пролета при Z=11м:
Определим углы поворота на опорах:
Переведем в градусы, умножив на
Определим максимальный относительный прогиб в пролете балки:
Условие жесткости выполняется.
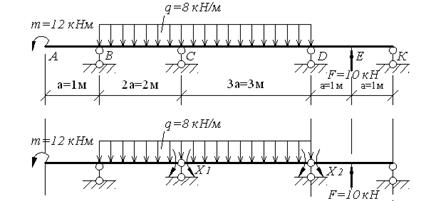
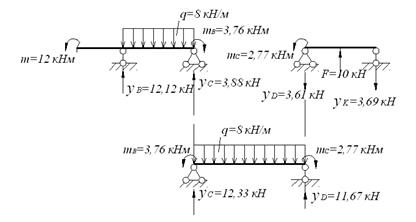
5. НЕРАЗРЕЗНЫЕ БАЛКИ. Задача 5.1. Многопролетная (неразрезная) балка нагружена расчетной нагрузкой. Материал балки – сталь с расчетным сопротивлением R=210МПа, Rc = 130МПа и модулем упругости Е = 210ГПа, m=12 кН·м, q=8 кН/м, F=10кН, а = 1м. Для данной балки требуется: - построить эпюру поперечных сил и изгибающих моментов; - подобрать сечение из прокатного двутавра; - определить прогибы посредине каждого пролета и показать на схеме балки очертание ее изогнутой линии. Решение. При расчете неразрезных балок удобно в качестве основной принимать систему, получаемую из заданной врезанием на промежуточных опорах шарниров. При таком выборе основной системы неразрезная балка распадается на отдельные однопролетные балки, имеющие по одной общей опоре. Лишними неизвестными являются изгибающие моменты в опорах сечения, которые определяются из условий отсутствия взаимных углов поворота сечений над шарнирами. Эпюры моментов от заданных нагрузок и опорных единичных моментов в каждом пролете строятся, как для свободной двухопорной балки (рис, 5.1). Находим степень статистической неопределимости системы. Балка имеет две избыточные связи. В качестве основной принимаем систему с врезанными на опорах В и С шарнирами (рис.5.1).
Рис. 5.1. Схема неразрезной балки. Основная система.
Строим эпюры изгибающих моментов от заданных нагрузок для каждого из участков балки. Участок АС
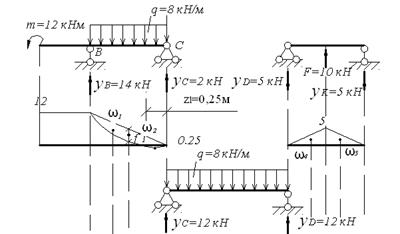
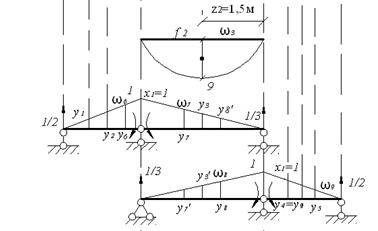
Рис. 5.2. Грузовые и одиночные эпюры, построенные в основной системе.
Рис. 5.3. Схема элементов балки с рассчитанными неизвестными.
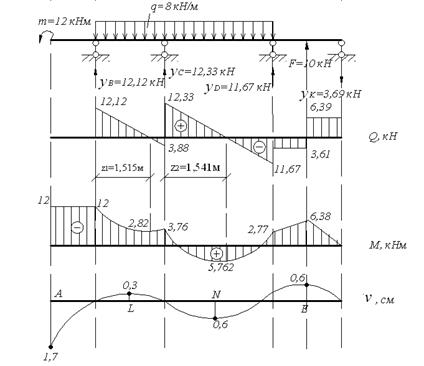
Рис. 5.4. Схема балки и эпюры поперечных сил и изгибающих моментов. Линия прогибов балки. Строим эпюру изгибающих моментов (рис.5.2): МА= -12кН· м, МВ=12кН ·м, Мс=0. Определим экстремальное значение изгибающего момента в пролете:
Участок CD:
Строим эпюру изгибающих моментов (рис.5.2): Мс=МD =0. Определим момент посредине пролета (
Участок DE:
Строим эпюру изгибающих моментов (рис.5.2):
|

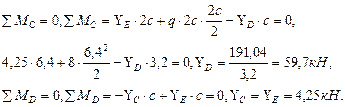
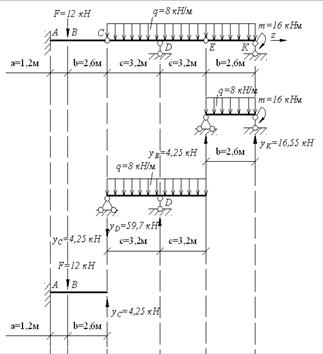
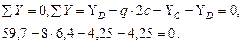
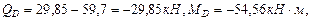
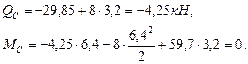
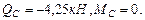
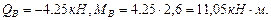
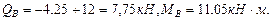
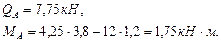
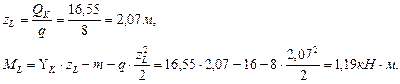
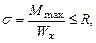
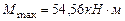 (из эпюры изгибающих
(из эпюры изгибающих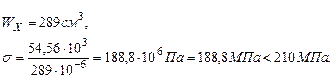
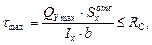
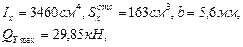
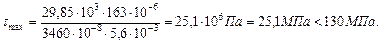
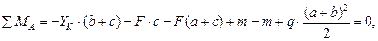
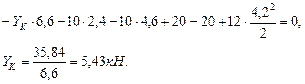
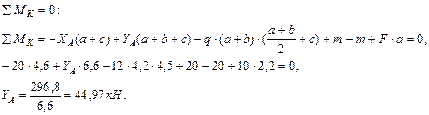
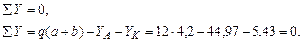
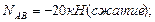
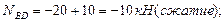
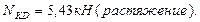
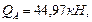 в точке В:
в точке В: 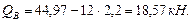
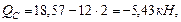 в точке D:
в точке D: 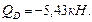
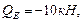 в точке D:
в точке D: 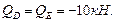
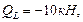 в точке В:
в точке В: 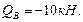
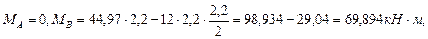 (растянутые волокна снизу)
(растянутые волокна снизу)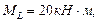 (растянутые волокна слева)
(растянутые волокна слева)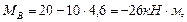 (растянутые волокна справа)
(растянутые волокна справа)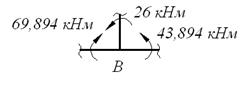
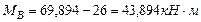 (растянутые волокна снизу).
(растянутые волокна снизу).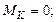
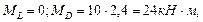 (растянутые волокна справа).
(растянутые волокна справа).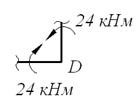
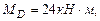 (растянутые волокна снизу)
(растянутые волокна снизу)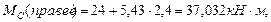
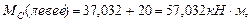 (растянутые волокна снизу).
(растянутые волокна снизу).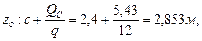
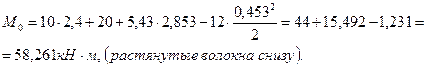
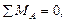


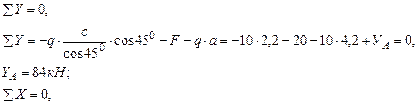
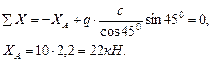
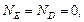
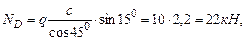 (растяжение).
(растяжение).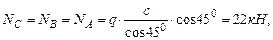 (растяжение).
(растяжение).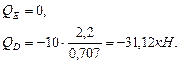
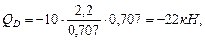
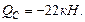
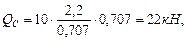
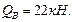
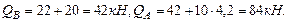
 (растянутые волокна слева),
(растянутые волокна слева),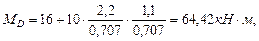 (растянутые волокна слева).
(растянутые волокна слева).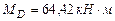 : (растянутые волокна слева),
: (растянутые волокна слева),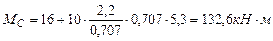 (растянутые волокна слева).
(растянутые волокна слева).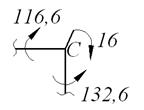
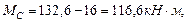 (растянутые волокна снизу),
(растянутые волокна снизу),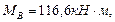 (растянутые волокна снизу).
(растянутые волокна снизу).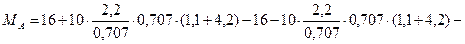
 (растянутые волокна).
(растянутые волокна).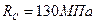 и модулем продольной упругости Е=200ГПа.
и модулем продольной упругости Е=200ГПа.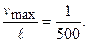

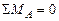 ;
;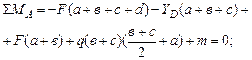
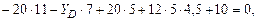
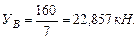
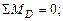
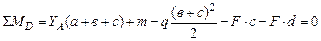
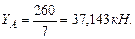
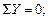
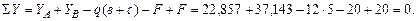 Строим эпюру поперечных сил (рис 4.13):
Строим эпюру поперечных сил (рис 4.13):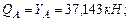
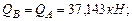
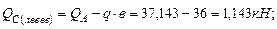
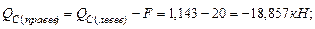
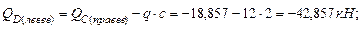
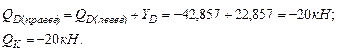
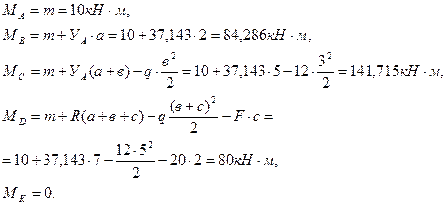 . Подберем сечение балки в виде двутавра, используя следующее условие прочности:
. Подберем сечение балки в виде двутавра, используя следующее условие прочности: 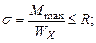 откуда требуемый момент сопротивления.
откуда требуемый момент сопротивления.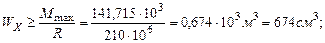
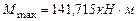 (согласно эпюре изгибающих моментов).
(согласно эпюре изгибающих моментов).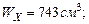
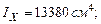
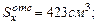
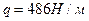 (собственный вес балки);
(собственный вес балки); 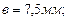
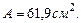
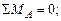
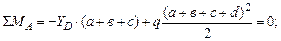
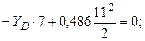
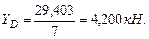
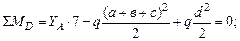
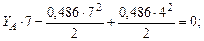
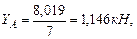
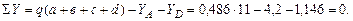
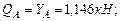
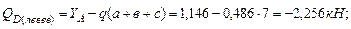
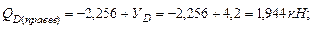
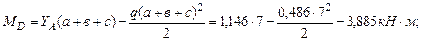

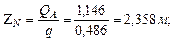
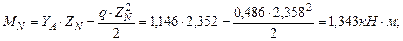
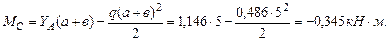

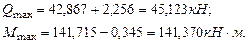
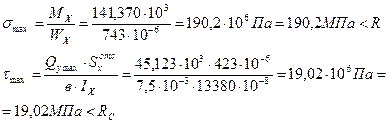
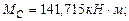
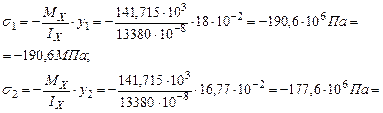
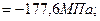 (сжатие)
(сжатие)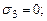
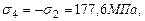 (растяжение);
(растяжение);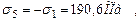 (растяжение);
(растяжение);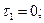 т.к.
т.к. 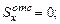
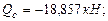
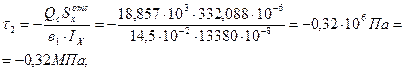
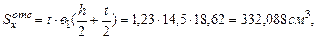
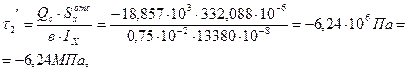
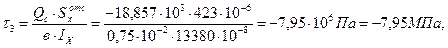
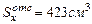 - статический момент площади половины сечения двутавра.
- статический момент площади половины сечения двутавра.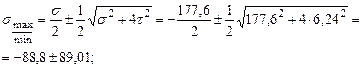
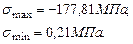
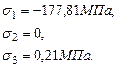
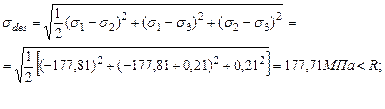
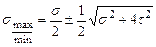
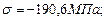
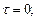
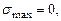
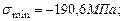
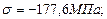
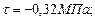
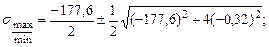
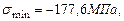
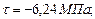
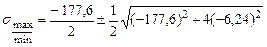
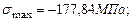
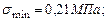
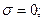
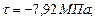
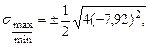
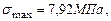
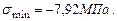
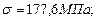

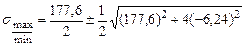
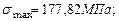
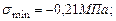
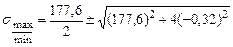
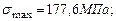
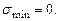
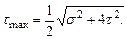
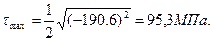
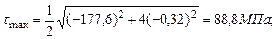
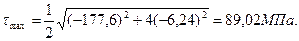
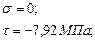
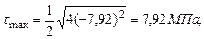
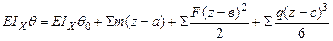
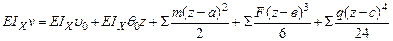 ,
,
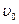 и
и 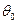 зададимся условием, что прогиб на опоре D равен 0.
зададимся условием, что прогиб на опоре D равен 0.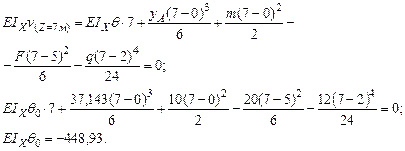
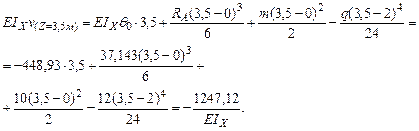
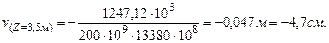
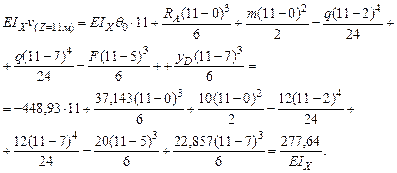 Так как распределенная нагрузка q действует не до конца балки, то продляем ее до точки К, приложив на участке DK q с обратным знаком.
Так как распределенная нагрузка q действует не до конца балки, то продляем ее до точки К, приложив на участке DK q с обратным знаком.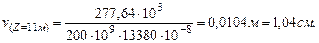
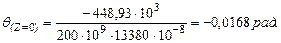
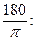
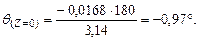
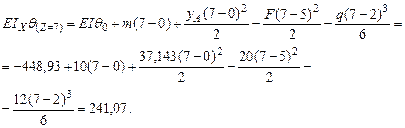
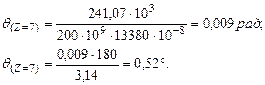
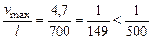
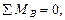
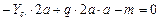 ,
, 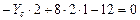 ,
,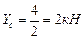 .
.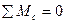 ,
, 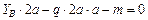 ,
, 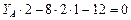 ,
,
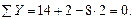
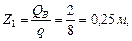
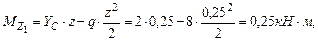
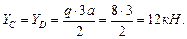

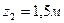 ):
):