Введение 4 страница
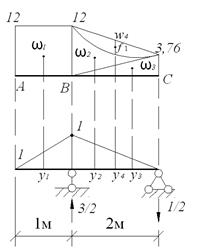
Построим единичные эпюры от опорных единичных моментов (рис.5.2): Х1=Х2=1. Канонические уравнения метода сил будут иметь следующий вид:
Вычислим площади грузовых и единичных эпюр:
Определим значение ординат единичных эпюр, расположенных под центрами тяжести соответствующих им грузовых эпюр:
Применяя правило Верещагина, определим коэффициенты канонического уравнения метода сил:
Если грузовая и единичная эпюры имеют разные знаки, то перед произведением площади эпюры на ординату под центром ее тяжести ставится знак «минус». Решаем систему канонических уравнений:
Для построения эпюры поперечных сил определим реакции опор. Рассмотрим равновесие всех пролетов раздельно, прикладывая к ним, кроме заданной нагрузки, найденные опорные моменты (рис.5.3, 5.4). Участок АС:
Участок CD:
Участок DK:
Заменяя опоры реакциями, строим эпюру поперечных сил. На опорах C и D суммируем реакции (рис. 5.4).
Строим эпюру изгибающих моментов (рис. 5.4): Определим значение изгибающих моментов в точках z1 и z2:
Проведем проверку правильности расчетов. Перемножаем окончательную эпюру изгибающих моментов на единичные (рис. 5.5).
Рис.5.5 Эпюра изгибающих моментов и единичные эпюры.
Используя сортамент (Приложение 1), выбираем двутавр №12, Wх = 58,4см3.
Недогрузка балки составляет:
Определим прогибы посредине каждого пролета балки. Для этого в основной системе в каждом пролете приложим единичную силу и построим единичные эпюры (рис.5.6, 5.7, 5.8, 5.9). Осуществим перемножение грузовой эпюры на единичную. Рассмотрим каждый участок балки:
Участок АС Определим площади элементов эпюры изгибающих моментов и значения ординат под их центрами тяжести.
Прогиб в точке А равен:
Участок ВС. Определим величину изгибающего момента в точке L:
Рис.5.7. Грузовая и единичная эпюры участка балки ВС. Площади элементов эпюры и ординаты под центрами их тяжести рассчитываем аналогично:
Прогиб в точке L равен:
Рис.5.8. Грузовая и единичная эпюры участка балки СD. Участок С D Определим значение изгибающего момента в точке N:
Площади элементов эпюры и ординаты под центрами их тяжести:
Прогиб в точке N:
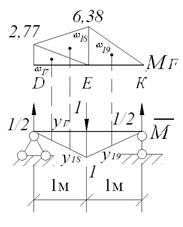
Рис.5.9. Грузовая и единичная эпюры участка балки DK.
Участок DK. Определим площади элементов эпюры изгибающих моментов на участке и ординаты под центрами их тяжести:
Прогиб в точке Е:
Подберем сечение балки из прокатного двутавра. Условие прочности:
По сортаменту (Приложение 1) подбираем двутавр №12
Балка недогружена: Проверим балку по касательным напряжениям:
Построим изогнутую ось балки, определив прогибы в пролетах:
Отразим изогнутую ось балки (рис.5.4).
Задача 5.2
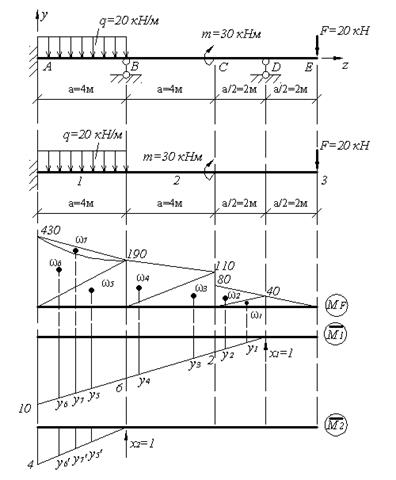
Многопролетная (неразрезная) балка нагружена расчетной нагрузкой. Материал балки – сталь с расчетным сопротивлением R=210МПа, Rc=130МПа и модулем упругости Е=210ГПа, m=12 кН·м, q=8 кН/м, F=10кН, а = 1м.
Рис.5.10. Схема балки и основной системы. Грузовая и единичные эпюры основной системы.
Рис.5.11. Эпюры поперечных сил и изгибающих моментов. Единичные эпюры. Линия прогибов балки. Данная балка имеет две избыточные связи сверх необходимого минимума для обеспечения неизменяемости схемы. Канонические уравнения будут иметь вид:
Лишними неизвестными являются реакции опор В и D. В качестве основной принимаем систему, имеющую заделку в точке А. Построим эпюру изгибающих моментов от действующей нагрузки (рис.5.10):
Построим эпюры изгибающих моментов от единичных сил, приложенных вместо отброшенных связей (рис.6.10):
Определим площади участков грузовой эпюры изгибающих моментов (
Определяем члены канонического уравнения:
Решаем систему уравнений:
Откуда находим, что Строим эпюры поперечных сил и изгибающих моментов:
Определим значение изгибающего момента в точке N.
Осуществим проверку правильности расчетов, перемножив конечную эпюру изгибающих моментов на единичные .
Определим прогибы посредине каждого из пролетов и в точке Е. Для этого воспользуемся методом начальных параметров.
Запишем выражение начальных параметров для Z=2м, Z=6м, Z=12м.
Подберем сечение в виде двутавра (Приложение 1): R=200МПа, Подберем по сортаменту двутавр №22, Прогиб в точке 1 при Z=2: при Z=6: при Z=12: Строим изогнутую линию балки (рис.5.11).
6. СЛОЖНОЕ СОПРОТИВЛЕНИЕ.
Задача 6.1. Внецентренное сжатие.
Колонна заданного поперечного сечения сжимается расчетной силой F, направленной параллельно продольной оси и приложенной к точке К. Расчетные сопротивления для материала колонн: на растяжение Требуется: 1) найти положение нулевой линии; 2) вычислить наибольшие сжимающие и растягивающие напряжения и построить эпюру напряжений, дать заключение о прочности колонны; 3) построить ядро сечения
F=80 кН; a=20 см; b=12 см.
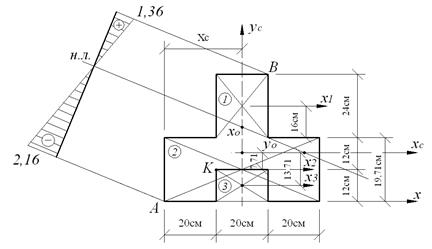
Рис. 6.2. Положение центра тяжести и нулевой линии. Решение. Определим координаты тяжести сечения. Поперечное сечение колонны имеет ось симметрии
где
Определим геометрические характеристики сечения. Для вычисления главных центральных моментов инерции воспользуемся зависимостью между моментами инерции при параллельном переносе осей.
Определим квадраты радиусов инерции:
Координаты точки приложения силы F:
Положение нулевой линии:
По найденным отрезкам, отсекаемых на осях координат, проводим нулевую линию (рис 6.2). Определим наибольшие сжимающие и растягивающие напряжения. Наиболее удаленными от нулевой линии точками являются точки А и В. Их координаты:
Напряжения в этих опасных точках не должны превосходить соответствующего расчетного сопротивления:
Знак минус перед формулой показывает, что сила, приложенная к колонне, является сжимающей. Нулевая линия делит сечение на зоны сжатия (область приложения силы F) и растяжения. Растягивающее напряжение:
По результатам напряжений Построим ядро сечения (рис. 6.3).
Рис. 6.3. Ядро сечения. Чтобы получить очертание ядра сечения, необходимо рассмотреть все возможные положения касательных к контуру сечения и, предполагая, что эти касательные являются нулевыми линиями, вычислить координаты граничных точек ядра относительно главных центральных осей сечения. Соединяя затем эти точки, получим очертание ядра сечения. Касательная 1-1:
Касательная 2-2:
Касательная 3-3: Определим координаты точек пересечения секущей 3-3:
Касательная 4-4:
Поскольку сечение имеет ось симметрии
Задача 6.2. Косой изгиб.
Балка нагружена в главных плоскостях расчетной нагрузкой. Материал балки – сталь с расчетным сопротивлением R=210Мпа. Требуется: 1) построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях; 2) определить опасное сечение и подобрать двутавр, приняв 3) определить положение нейтральной оси в одном сечении и построить эпюру нормальных напряжений.
Рис.6.4. Схема балки.
Решение. Определим вертикальные и горизонтальные опорные реакции и строим
Рис 6.5. Эпюры изгибающих моментов относительно осей Х и Y.
Выберем наиболее опасное сечение. Максимальные моменты в плоскости оси Х и Y находятся в точке А: Определим требуемый момент сопротивления, приняв Условие прочности при косом изгибе для балок из материала, одинаково сопротивляющегося растяжению и сжатию, имеет следующий вид:
По сортаменту (Приложение 1) принимаем двутавр №40, Проверяем прочность балки:
Прочность балки обеспечена. Недогрузка балки составляет: Определяем угол наклона нулевой линии к оси ОХ:
Рис. 6.6. Положение нулевой линии. Эпюра напряжений.
Для построения эпюры Угол наклона силовой линии:
Задача 7.3. Общий случай нагружения.
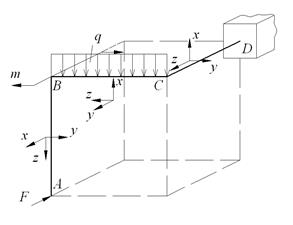
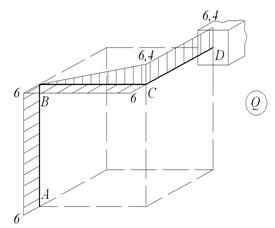
Пространственная система, состоящая из трех стержней, жестко соединенных между собой под прямым углом, нагружена расчетной нагрузкой в вертикальной и горизонтальной плоскостях. Стержни системы имеют одинаковые длины и диаметры поперечных сечений. Материал стержней – сталь с расчетным сопротивлением R =210МПа и Rc =130МПа, m = 4кН м, ℓ=0,8м, q = 8кН/ м, d = 10см, F = 6кН. Требуется: 1) построить эпюры внутренних усилий; 2) установить вид сопротивления для каждого участка стержня; 3) определить опасное сечение и дать заключение о прочности конструкции.
Рис. 6.7. Схема пространственной системы.
Решение. Построим эпюру продольных сил. На участках АВ и ВС отсутствуют продольные силы. Участок С D: Продольной силой для данного участка является сила F. N=-F=-6кН (сжатие) (рис 6.8).
Рис. 6.8. Эпюра продольных сил.
Построим эпюру поперечных сил (рис 7.9). Участок А B:
Участок ВС:
Участок С D:
Рис. 6.9. Эпюра поперечных сил.
Построим эпюру изгибающих моментов. Для этого последовательно построим эпюры от каждого вида нагрузки. Сила F: Участок АВ:
Участок ВС:
Участок С D:
|

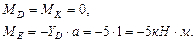


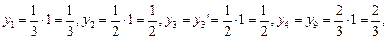

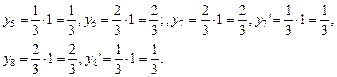


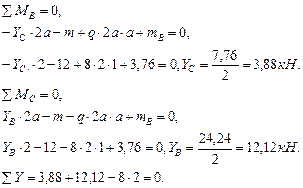


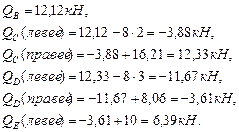

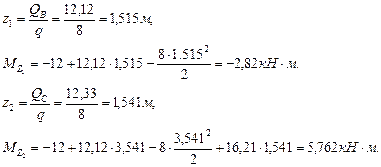

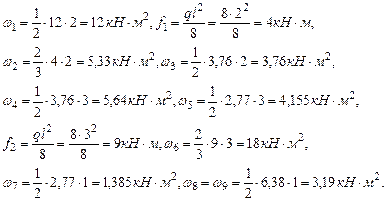

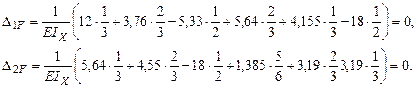 Подберем сечение в виде двутавра:
Подберем сечение в виде двутавра: 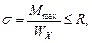


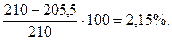 Проверим балку по касательным напряжениям:
Проверим балку по касательным напряжениям: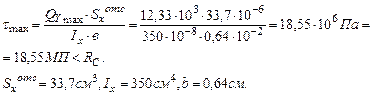

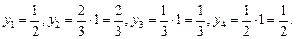
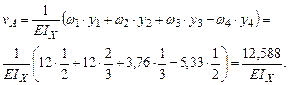
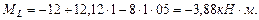










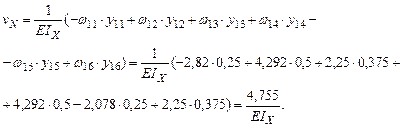

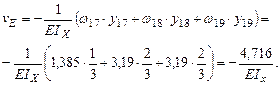

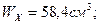
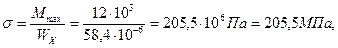

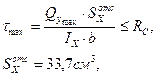

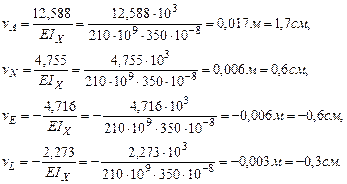



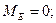
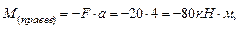
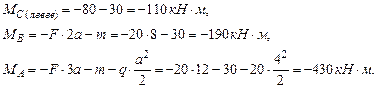
 (от силы
(от силы  ,
, (от силы
(от силы  .
.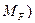 и ординат под центрами их тяжести в единичных эпюрах (
и ординат под центрами их тяжести в единичных эпюрах (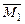 и
и 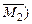 .
.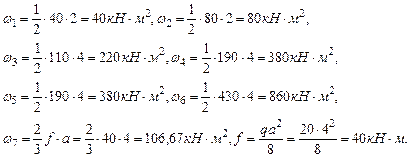


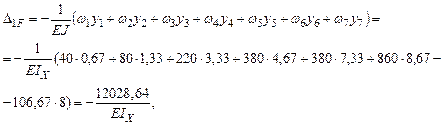


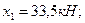

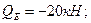
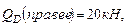

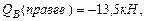

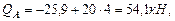
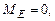
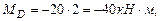
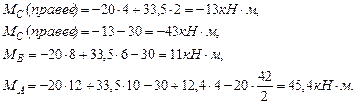
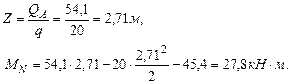


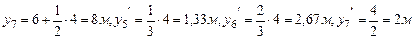
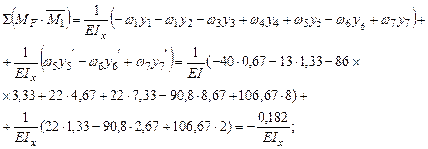 Ошибка составляет 0,016%
Ошибка составляет 0,016%
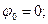
 в начале координат.
в начале координат.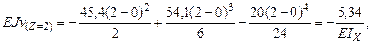
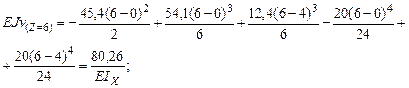
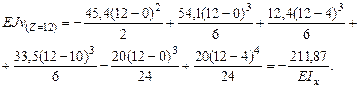

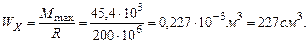
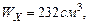
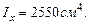
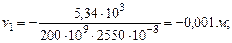


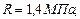 на сжатие
на сжатие 
 .
.
 , следовательно, центр тяжести лежит на этой оси и для отыскания координаты
, следовательно, центр тяжести лежит на этой оси и для отыскания координаты  относительно вспомогательной оси
относительно вспомогательной оси  , сложное сечение разбиваем на три прямоугольника.
, сложное сечение разбиваем на три прямоугольника.
 ,
,  и
и  - координаты центров тяжести прямоугольников относительно оси
- координаты центров тяжести прямоугольников относительно оси  , а
, а ,
,  и
и  - площади их поперечных сечений.
- площади их поперечных сечений.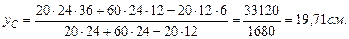
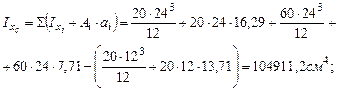
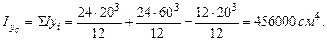
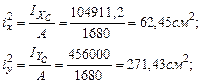


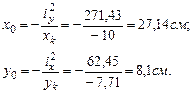
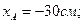


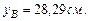

 Сжимающие напряжение:
Сжимающие напряжение: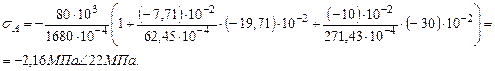 Прочность колонны обеспечена.
Прочность колонны обеспечена.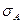 и
и  строим эпюру
строим эпюру  (рис. 6.2)
(рис. 6.2)
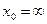 ;
; 
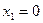 ;
; 
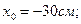
 ;
;
 .
.







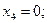



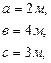
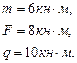
 и
и  (рис.6.2)
(рис.6.2)
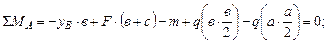

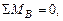




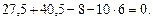
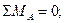




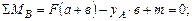
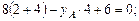
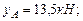
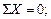



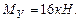
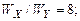 т.е.
т.е. 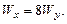
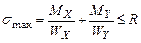 или
или 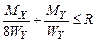 , откуда
, откуда


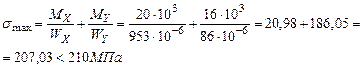
 .
.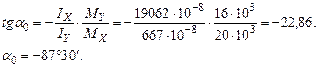

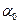 откладываем против часовой стрелки от оси ОХ. Наибольшие напряжения будут действовать в угловых точках сечения, причем в точке А они будут растягивающими, а в В – сжимающими.
откладываем против часовой стрелки от оси ОХ. Наибольшие напряжения будут действовать в угловых точках сечения, причем в точке А они будут растягивающими, а в В – сжимающими.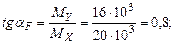



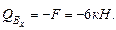
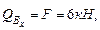

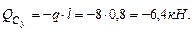
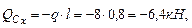

 =0,
=0, 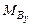 =F· ℓ = 6· 0,8=4,8кН· м.
=F· ℓ = 6· 0,8=4,8кН· м.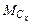 = F· ℓ= 6· 0,8= 4,8кН·м.
= F· ℓ= 6· 0,8= 4,8кН·м.


