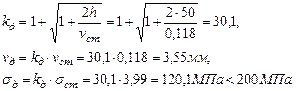Введение 5 страница
Изгибающий момент m: Участок ВС:
Участок С D:
Распределенная нагрузка q:
Участок ВС:
Участок С D:
Рис. 6.10. Эпюра изгибающих моментов от действия силы F.
Рис. 6.11. Эпюра изгибающих моментов от действия изгибающего момента m.
Рис. 6.12. Эпюра изгибающих моментов от действия равномерно распределенной нагрузки q.
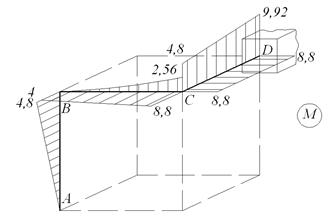
Просуммируем изгибающие моменты от всех видов нагрузки.
Рис. 6.13. Суммарная эпюра изгибающих моментов от действия всех видов нагрузки.
Построим эпюру крутящих моментов.
Участок ВС:
Участок С D:
Рис. 6.14. Эпюра крутящих моментов.
Установим вид сопротивления для каждого участка системы, который определяется по эпюрам. На участке АВ действует поперечная сила Qx и изгибающий момент My (поперечный изгиб). На участке ВС действует поперечная сила Qx, Qy, крутящий момент Т и изгибающие моменты Mx и My (косой изгиб с кручением). На участке СD действует поперечная сила Qx, крутящий момент Т, изгибающие моменты Mx, My и продольная сила N (косой изгиб с кручением и сжатием). Определим максимальные напряжения в опасном сечeнии каждого участка от внутренних усилий Mx,My,T,N (касательными напряжениями от поперечных сил Qx и Qy можно пренебречь). Участок АВ: Опасная точка В. Qx =6кН,My =4,8кН· м.
Участок ВС: Опасная точка С. Qy = 6кН, Qx = 6,1кН, Mx =8,8кН·м, My=2,56кН ·м, Т=4,8кН ·м. Определим суммарный изгибающий момент:
При кручении круглого стержня возникают касательные напряжения:
Участок С D: Опасная точка D. Qx=6,4кН, Mx=8,8кН· м, My=9,92кН· м, N=6кН, Т=2,56кН· м.
Проверим прочность системы при расчетном сопротивлении R =210Мпа. Расчетное напряжение по третьей теории прочности для плоского напряженного состояния определяется по формуле:
Участок АВ:
Участок ВС:
Участок С D:
Прочность стержней системы на всех участках обеспечена.
7. УСТОЙЧИВОСТЬ. Задача 7.1. Стальной стержень сжимается продольной расчетной нагрузкой F. Расчетное сопротивление материала стержня R=200МПа, модуль продольной упругости Е=200ГПа. Требуется: 1) подобрать размеры поперечного сечения стержня из условия устойчивости; 2) определить значение коэффициента запаса устойчивости.
F=210кН; l=1,7 м; µ=1. Решение. Размеры поперечного сечения определим исходя из условий устойчивости:
где В расчетной формуле имеются две неизвестные величины – коэффициент Выразим геометрические характеристики через величину а. Так как потеря устойчивости происходит в плоскости наименьшей жесткости, определяем минимальный момент инерции:
тогда площадь поперечного сечения:
Приближение 1. В первом приближении коэффициент изгиба принимают
Расчетная гибкость стержня:
По таблице (Приложение 5) определяем значение коэффициента
Путем линейной интерполяции получим:
Проверим выполнение условия устойчивости в первом приближении:
Перенапряжение составляет Приближение 2. За новое значение коэффициента
тогда площадь сечения
радиус инерции
Определим гибкость стержня
Коэффициент
Проверим выполнение условий устойчивости:
Перенапряжение составляет: Приближение 3. Определим коэффициент продольного изгиба:
Площадь поперечного сечения
радиус инерции гибкость колонны Определим значение коэффициента
Расчетное сопротивление
Недонапряжение составляет Окончательно принимаем размеры сечения 44х66мм (
Находим величину критической силы. Так как
Определим коэффициенты запаса устойчивости:
Задача 7.2
Стальной стержень сжимается продольной расчетной нагрузкой F. Расчетное сопротивление материала стержня R=200МПа, модуль продольной упругости Е=200ГПа. Требуется: 1) подобрать размеры поперечного сечения стержня из условия устойчивости; 2) F=250 кН; l=1,4 м; µ=2.
Решение. Определим размеры поперечного сечения исходя из условия устойчивости:
Для расчета используем метод последовательных приближений. Приближение 1. В первом приближении примем коэффициент продольного изгиба
Площадь одного уголка составит:
Из сортамента прокатной стали (Приложение 3) выбираем уголок 100х100х6,5 с площадью А уг= 12,8см. Определим радиусы инерции данного сечения относительно главных центральных осей х и у, которые являются осями симметрии сечения.
(
Сравнивая Определим гибкость колонны:
По таблице (Приложение 5) определяем значение коэффициента при
Путем линейной интерполяции получим:
Проверим выполнение условия устойчивости в первом приближении:
Перенапряжение составляет Необходимо увеличить поперечное сечение. . Приближение 2. За новое значение коэффициента
В сортаменте выбираем уголок 110х110х7 Определяем гибкость стержня:
Из таблицы для
Проверим выполнение условий устойчивости:
Недонапряжение составит: Окончательно принимаем сечение в виде двух уголков 110х110х7. Находим величину критической силы. Так как
Тогда коэффициент запаса устойчивости будет равен:
8. ДИНАМИКА. Задача 8.1.
На упругую систему падает груз Требуется: 1) определить величины максимальных динамических напряжений в элементах системы; 2) определить величину динамического перемещения точки приложения груза.
G=400H, в=0,4м, d=4см, а=1,4м, двутавр №18, h=5см.
Решение. Рассчитаем стержневую систему на статическую нагрузку Предварительно определим усилие в стержне.
Рис.8.2 Схема элемента 1. Составим уравнение равновесия
Рассчитаем опорные реакции в балке ВС:
Рис.8.3 Схема балки.
Построим эпюру изгибающих моментов в балке ВС:
Рис.8.4. Эпюра изгибающих моментов и единичная эпюра. Определим прогиб в точке D от статического действия нагрузки методом сил. Для этого приложим в точке D единичную силу и построим эпюру изгибающих моментов от этой силы.
Прогиб от статистической нагрузки составит:
. Определим напряжение от статической нагрузки:
Определим динамический коэффициент, динамическое перемещение и напряжение:
Проведем проверку стержня на прочность при действии динамической нагрузки:
Литература
1. Александров, А.В. Сопротивление материалов / А.В. Александров, В.Д. Потапов, Б.П. Державин. – М.: Высш. школа, 1995. 2. Балыкин, М.К. Сопротивление материалов: сборник заданий для расчетно-проектировочных работ для строительных специальностей / М.К. Балыкин [и др.]. – Минск: БНТУ, 2003. 3. Винокуров, Е.Ф. Сопротивление материалов: расчетно-проектировочные работы / Е.Ф. Винокуров, А.Г. Петрович, Л.И. Шевчук. – Минск: Вышэйшая школа, 1987. 4. Заяц, В.Н. Сопротивление материалов / В.Н. Заяц, М.К. Балыкин, И.А. Голубев. – Минск: БГПА, 1998. 5. Петрович, А.Г. Сборник задач расчетно-проектировочных работ по курсу «Сопротивление материалов»: в 2 ч. / А.Г. Петрович [и др.]. – Минск: БПИ, 1979. – Ч. 1. 6. Петрович, А.Г. Сборник задач расчетно-проектировочных работ по курсу «Сопротивление материалов»: в 2 ч. / А.Г. Петрович 7. Писаренко, Г.С. Сопротивление материалов / Г.С. Писаренко [и др.]. – Киев: Вища школа, 1986. 8. Смирнов, А.Ф. Сопротивление материалов / А.Ф. Смирнов 9. Феодосьев, В.И. Сопротивление материалов / В.И. Феодосьев. – М.: Наука, 1986. 5. Балыкин, М.К. Сопротивление материалов: лабораторный практикум / М.К. Балыкин [и др.]. – Минск: БГПА, 1999. 10. Нагрузка и воздействие: СНиП 2.01.07-85. – Госстрой СССР, 1985.
Приложения Приложение 1 Сталь горячекатаная. Балки двутавровые (по ГОСТ 8239-89*)
I – момент инерции W – момент сопротивления S – статический момент площади полусечения i – радиус инерции
Таблица П1.1
Приложение 2 Сталь горячекатаная. Швеллерная (по ГОСТ 8240-89)
I – момент инерции
|

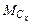 = 4,8кН·м,
= 4,8кН·м, 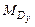 = 4,8кН·м,
= 4,8кН·м, = 4,8кН·м.
= 4,8кН·м. = 4кН·м,
= 4кН·м, = 4кН·м.
= 4кН·м.
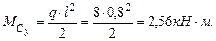
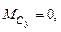
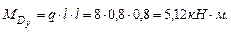

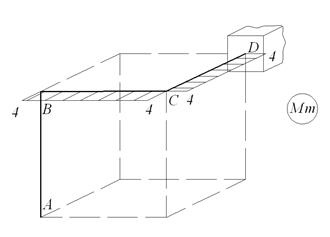

 Участок АВ:
Участок АВ:
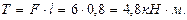
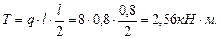

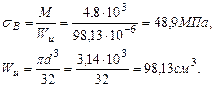

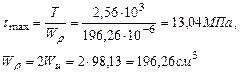
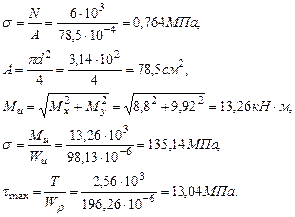
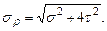
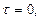
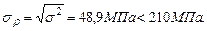
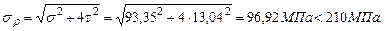
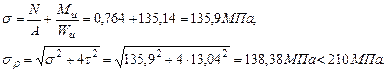


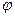 - коэффициент снижения расчетного сопротивления материала при продольном изгибе.
- коэффициент снижения расчетного сопротивления материала при продольном изгибе.

 тогда
тогда


 соответствующего гибкости
соответствующего гибкости  :
: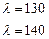
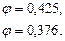
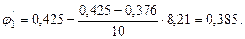
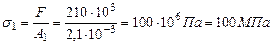 ,
,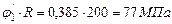 .
.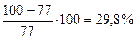 , что недопустимо. Необходимо уточнение размеров.
, что недопустимо. Необходимо уточнение размеров. принимаем среднее арифметическое первых двух:
принимаем среднее арифметическое первых двух: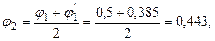
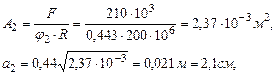


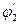 рассчитываем для гибкости
рассчитываем для гибкости  :
:
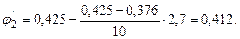
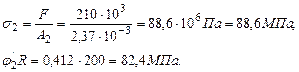
 что недопустимо.
что недопустимо.
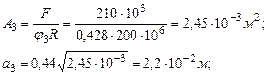
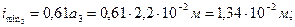
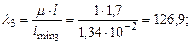
 :
: 



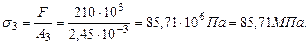

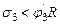

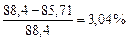 , что допустимо.
, что допустимо.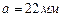 )
)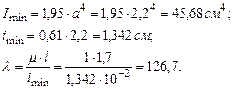
 , т.е.126,7>100, то используем формулу Эйлера для определения критической силы:
, т.е.126,7>100, то используем формулу Эйлера для определения критической силы:
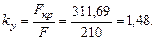
 определить значение коэффициента запаса устойчивости;
определить значение коэффициента запаса устойчивости; .
. , тогда
, тогда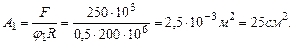
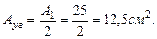
 (находим в сортаменте, Приложение 3).
(находим в сортаменте, Приложение 3).
 (находим в сортаменте, Приложение 3),
(находим в сортаменте, Приложение 3),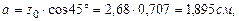
 находим в сортаменте),
находим в сортаменте),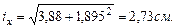
 и
и  ,определяем, что минимальным радиусом инерции является
,определяем, что минимальным радиусом инерции является 
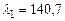 :
:
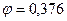

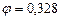


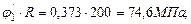
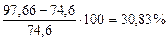 , что недопустимо.
, что недопустимо.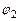 принимаем среднее арифметическое первых двух.
принимаем среднее арифметическое первых двух.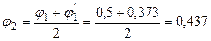 ; тогда площадь сечения
; тогда площадь сечения

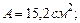
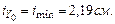
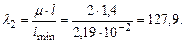
 выберем значение
выберем значение  :
:


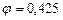




 , что для прокатного профиля приемлемо.
, что для прокатного профиля приемлемо.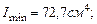
 , т.е. 127,9>100, то используем формулу Эйлера для определения критической силы:
, т.е. 127,9>100, то используем формулу Эйлера для определения критической силы:
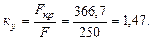
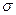 с высоты h. Материал стержней – сталь. Расчетное сопротивление при статической нагрузке R=210МПа, Е=200ГПа.
с высоты h. Материал стержней – сталь. Расчетное сопротивление при статической нагрузке R=210МПа, Е=200ГПа. Массу конструкции не учитывать.
Массу конструкции не учитывать.
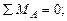
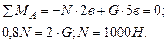

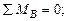


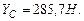

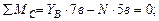
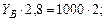

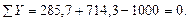

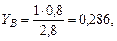


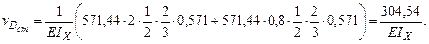 Выпишем из сортамента значение момента инерции для двутавра №18:
Выпишем из сортамента значение момента инерции для двутавра №18: 
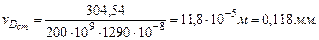
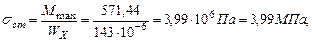
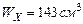 (выпишем из сортамента, Приложение 1).
(выпишем из сортамента, Приложение 1).