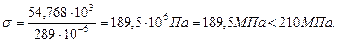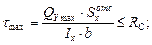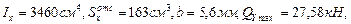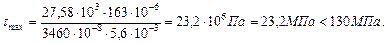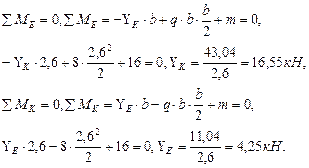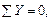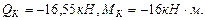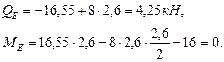Введение 2 страница
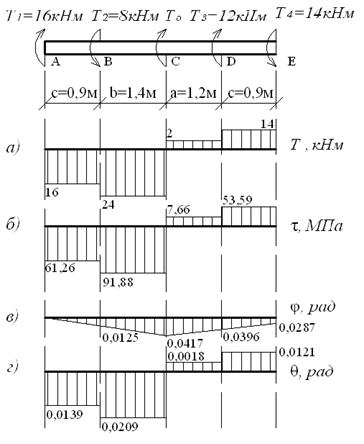
Рис 3.2.Эпюры крутящих моментов, касательных напряжений, углов закручивания и относительных углов закручивания.
Построим эпюру крутящих моментов. При определении крутящих моментов в сечениях вала, принимаем следующее правило знаков: момент считается положительным, если при взгляде со стороны сечения его направление совпадает с движением часовой стрелки. Участок АВ: Участок ВС: Участок СD: Участок DE: По эпюре определяем максимальный крутящий момент:
Определим диаметр вала из условия прочности.
где
Определим диаметры вала из условия жесткости.
Из двух значений диаметров выбираем большее, округлив до 0,09м: Определим касательные напряжения, действующие в сечениях.
Участок АВ. Участок ВС:
Участок СD:
Участок DE:
Построим эпюру касательных напряжений (рис.3.2б).
Определим углы закручивания на участках вала. Используем следующую формулу:
Определим относительные углы закручивания на участках вала. Для расчета используем формулу
Построим эпюру относительных углов закручивания (рис.3.2.г) Наиболее загруженным является участок DE, где Условие прочности выполняется.
Задача 3.2.
Стальной вал круглого поперечного сечения нагружен скручивающими моментами. Расчётное сопротивление материала вала на сдвиг Rc=130 МПа, а модуль сдвига G=80 ГПа. Требуется: 5) подобрать диаметр вала; 6) построить эпюру крутящих моментов и напряжений; 7) построить эпюру углов закручивания; 8) построить эпюру относительных углов закручивания.
а= 1,2м; в =1,4м; с =0,9м;
Рис. 3.3.Схема вала. Эпюры крутящих моментов, касательных напряжений, углов закручивания и относительных углов закручивания. Построим эпюру крутящих моментов. Выберем начало координат в точке А, предположив, что вал имеет защемление в этой точке. Определим величину уравнения неизвестного момента
Участок АВ: Участок ВС: УчастокCD: УчастокDE: По эпюре (рис 3.3а) определяем максимальный крутящий момент:
Определяем диаметр вала из условия прочности.
Определим диаметр вала из условия жесткости.
Из двух значений диаметров выберем большее, округлив до 0,11м.
Определим касательные напряжения, действующие в сечениях. Участок АВ:
Участок ВС:
Участок СD:
Участок DE:
Построим эпюру касательных напряжений (рис. 3.3б). Определим углы закручивания на участках вала. Используем формулу:
Определим относительные углы закручивания на участках вала. Для расчета используем формулу
Построим эпюру относительных углов закручивания (рис 3.3г). Наиболее загруженным является участок ВС, Условие прочности выполняется.
4. ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ.
З а д а ч а 4.1. Для указанной балки построить эпюры внутренних усилий. Выполнить расчёт на прочность. Подобрать двутавровое сечение из прокатного профиля, если R=210 МПа, Rc=130 МПа. m=20 кН·м, q=8 кН/м, F=12кН. Решение. Определим реакции опор. Составим уравнение равновесия:
Рис. 4.1. Схема балки. Эпюры поперечных сил и изгибающих моментов. Исходя из направления нагрузок ( Построим эпюры поперечных сил и изгибающих моментов методом сечений. В точке А: В точке В: В точке С (правее): В точке С (левее): В точке D:
Подберём двутавровое сечение при R=210 МПа.
Максимальный изгибающий момент Mmax определим по эпюре изгибающих моментов (рис.4.1). Mmax = 170,08 кН·м.
Пользуясь сортаментом (Приложение 1), выбираем двутавр №40 с Wx=953 см3. Проверим прочность по нормальным напряжениям:
Проверим прочность по касательным напряжениям:
З а д а ч а 4.2. Для указанной балки (рис.4.2) построить эпюры внутренних усилий. Подобрать сечение из двух швеллеров из прокатных профилей, если R=210 МПа, Rc=130 МПа. m=18 кН·м, q=20 кН/м, F=12кН.
Рис. 4.2. Схема балки. Эпюры поперечных сил и изгибающих моментов. Решение. Определим реакции опор. Составим уравнение равновесия:
Проверим правильность определения реакций:
Построим эпюры поперечных сил и изгибающих моментов методом сечений (рис.5.2). В точке А: В точке В (левее): В точке В (правее): В точке С (левее): В точке С (правее): В точке D(левее)
В точке Е эпюра поперечных сил пересекает ось z. Определим значение изгибающего момента в этой точке. Определим расстояние Z0:
Подберём сечение в виде двух швеллеров (Приложение 2) при R=210 МПа.
Для одного швеллера: Проверим прочность по нормальным напряжениям:
Перегрузка составляет:
Проверим прочность по касательным напряжениям:
З а д а ч а 4.3. Для указанной балки построить эпюры внутренних усилий. Выполнить расчёт на прочность. Подобрать прямоугольное сечение из древесины, если соотношение сторон сечения составляют m=8 кН·м, q=6 кН/м, F=8кН.
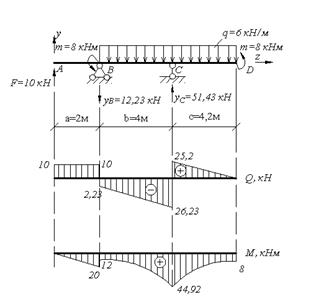
Рис. 4.3. Схема балки. Эпюры поперечных сил и изгибающих моментов.
Решение. Определим реакции опор. Составим уравнение равновесия:
Проверим правильность определения реакций:
Построим эпюры поперечных сил и изгибающих моментов (рис.5.3): В точке А: В точке В (левее): В точке В (правее): В точке С (левее): В точке С (правее): В точке D: Подберём прямоугольное сечение,
Округляем
Недогрузка составляет:
Проверим прочность по касательным напряжениям:
Прочность деревянной балки по нормальным и касательным напряжениям обеспечена.
З а д а ч а 4.4.
Для указанной балки (рис.5.4) построить эпюры внутренних усилий. Выполнить расчёт на прочность. Подобрать круглое сечение из древесины, если R=16 МПа, RC=2 МПа, m=20 кН·м, q=10 кН/м, F=16кН.
Решение.
Рис.4.4. Схема балки. Эпюры поперечных сил и изгибающих моментов. Проверим правильность определения реакций:
Построим эпюры поперечных сил и изгибающих моментов. В точке А: В точке В (левее): В точке В (правее):
В точке С (левее): В точке С (правее): В точке D: Определим значение изгибающего момента в точке K и М (в этих точках эпюра поперечных сил меняет знак).
Подберём круглое сечение. Из эпюры изгибающих моментов (рис.4.4) выберем максимальный изгибающий момент.
Принимаем Определим максимальные нормальные напряжения:
Проверим прочность по касательным напряжениям:
рис.4.4)
З а д а ч а 4.5.
Для указанной балки построить эпюры внутренних усилий и проверить прочность. Поперечное сечение балки – двутавр № 30, R=210 МПа, RC=130 МПа, m=24 кН·м, q=16 кН/м, F=18кН.
Рис.4.5. Схема шарнирной балки. Эпюры поперечных сил и изгибающих моментов. Решение. Данная шарнирная балка может рассматриваться как сочетание консольной балки DE и подвесной двухопорной балки AD, для которой правой опорой является конец консоли D первой балки. Рассмотрим равновесие подвесной балки AD и определим ее опорные реакции:
Построим эпюры поперечных сил и изгибающих моментов. В точке А: В точке В (левее): В точке В (правее): В точке С (левее): В точке С (правее): В точке D:
Рассмотрим консольную балку DE. Реакцию YD прикладываем в точке D с противоположным знаком. Строим эпюры поперечных сил и изгибающих моментов с учётом YD. В точке D:
Определим величину изгибающих моментов в точках K и M (в данных точках эпюра поперечных сил меняет знак, рис.4.5):
Проверим прочность балки по нормальным напряжениям:
Недогрузка составляет:
Проверим прочность балки по касательным напряжениям:
Прочность двутавровой балки по нормальным и касательным напряжениям обеспечена.
З а д а ч а 4.6. Для указанной балки построить эпюры внутренних усилий и проверить прочность. Поперечное сечение балки – двутавр № 24, R=210 МПа, RC=130 МПа, m=10 кН·м, q=12 кН/м, F=20кН.
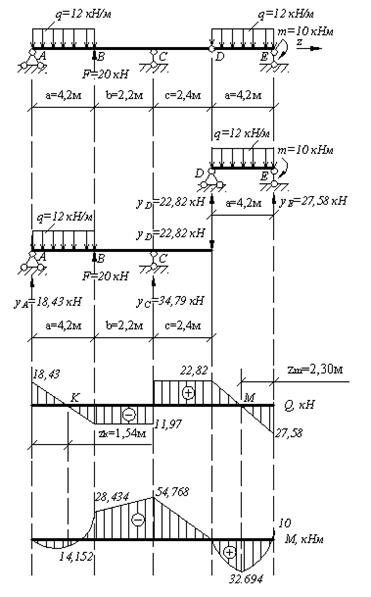
Рис.4.6. Схема шарнирной балки. Эпюры поперечных сил и изгибающих моментов. Решение. Данная шарнирная балка может рассматриваться как сочетание балки AD, лежащей на двух опорах и подвесной двухопрной балки DE. Рассмотрим равновесие подвесной балки DE. Определим реакции опор:
Проверяем правильность определения реакций опор:
Построим эпюры поперечных сил и изгибающих моментов на участке DE шарнирной балки. В точке Е: В точке D: Определим реакции опор балки AD, приложив в точку D реакцию YD, взятую с обратным знаком.
Построим эпюры поперечных сил и изгибающих моментов на участке AD шарнирной балки. В точке D: В точке С (правее):
В точке С (левее): В точке В (правее): В точке В (левее): В точке А:
Определим координаты точек К и М (zk и zm):
Вычислим значение изгибающих моментов в точках K и М:
Проверим несущую способность балки:
Прочность балки по нормальным напряжениям обеспечена. Проверим прочность балки по касательным напряжениям:
Для двутавра № 24 выпишем из сортамента (Приложение 1) геометрические характеристики сечения:
Прочность балки по касательным напряжениям обеспечена.
З а д а ч а 4.7.
Для указанной шарнирной балки построить эпюры внутренних усилий и проверить прочность. Поперечное сечение балки - двутавр № 24, R=210 МПа; RC=130 МПа, m=16 кН·м, q=8 кН/м, F=12кН. Решение. Данная балка может рассматриваться как сочетание балок КЕ, ЕС, последовательно лежащих на консоли АС. Рассмотрим равновесие подвесной балки КЕ. Определим реакции опор:
Проверим правильность определения реакций опор:
Построим эпюры поперечных сил и изгибающих моментов на участке КЕ шарнирной балки (рис.4.7). В точке K: В точке E:
|


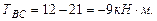
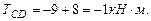
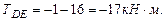
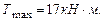
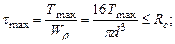
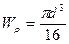 ;
;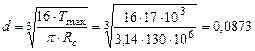 м.
м.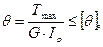 где
где 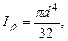
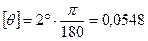 рад.
рад.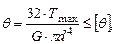
 м.
м.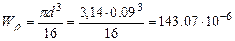
 .
.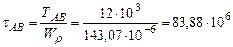 Па=83,88МПа.
Па=83,88МПа.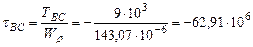 Па=-62,91МПа.
Па=-62,91МПа.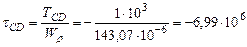 Па=-6,99МПа.
Па=-6,99МПа. Па=-118,82МПа.
Па=-118,82МПа.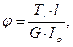 ;
; 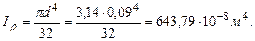
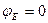 , т.к. угол поворота в заделке отсутствует.
, т.к. угол поворота в заделке отсутствует.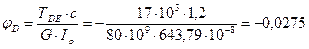 рад,
рад,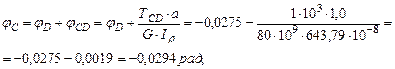
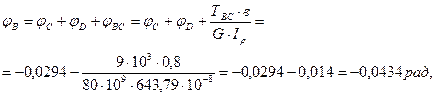
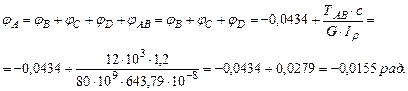 Построим эпюру углов закручивания (рис.3.2.в).
Построим эпюру углов закручивания (рис.3.2.в).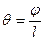 ;
;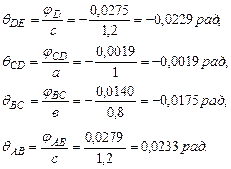
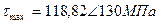
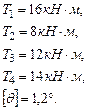
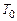 , составив уравнение равновесия:
, составив уравнение равновесия: 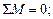
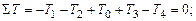
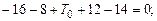
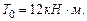
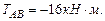
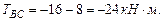
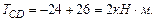
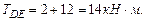
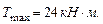
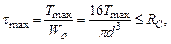 где
где 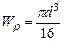 ,
,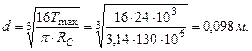
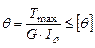 , где
, где 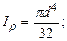
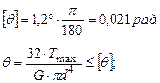

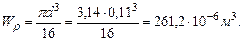
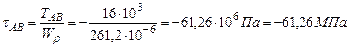
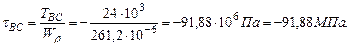
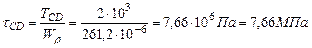
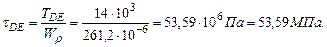
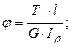
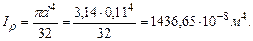
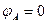 , (приняли в условии задачи, что т. А является неподвижной).
, (приняли в условии задачи, что т. А является неподвижной). Построим эпюру углов закручивания (рис. 3.3в).
Построим эпюру углов закручивания (рис. 3.3в).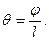
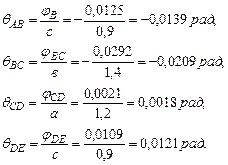
 .
.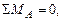
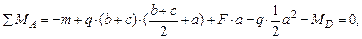

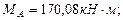
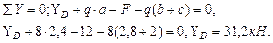

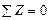 ) определяем, что горизонтальная реакция равна нулю.
) определяем, что горизонтальная реакция равна нулю.
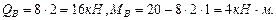
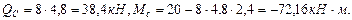
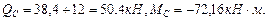

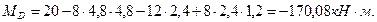
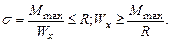

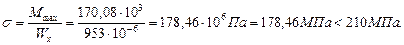 Недогрузка составляет:
Недогрузка составляет: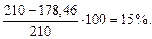
 Максимальное значение поперечной силы (QY max) определяем по эпюре поперечных сил (рис.4.1).
Максимальное значение поперечной силы (QY max) определяем по эпюре поперечных сил (рис.4.1).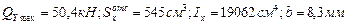 (геометрические характеристики выбираем из Приложения 1).
(геометрические характеристики выбираем из Приложения 1).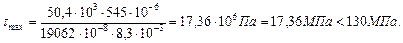 Прочность двутавровой балки по нормальным и касательным напряжениям обеспечена.
Прочность двутавровой балки по нормальным и касательным напряжениям обеспечена.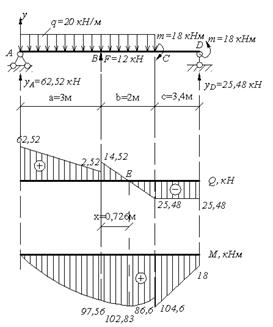
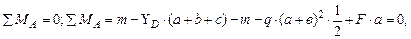
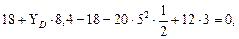
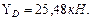
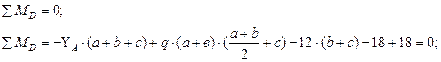
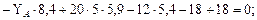
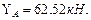
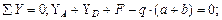
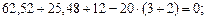

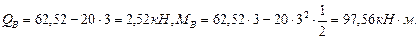

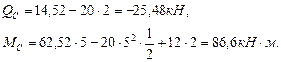
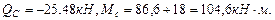

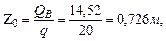

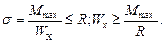
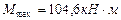 (из эпюры М, рис.4.2).
(из эпюры М, рис.4.2).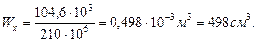
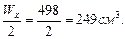 Из сортамента (Приложение 2) выбираем швеллер №24 с Wx=242 см3. Для двух швеллеров Wx=
Из сортамента (Приложение 2) выбираем швеллер №24 с Wx=242 см3. Для двух швеллеров Wx= 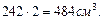
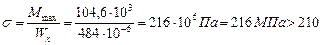 МПа.
МПа.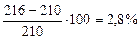 .
.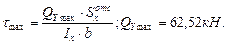
 (геометрические характеристики швеллера выбираем из Приложения 2).
(геометрические характеристики швеллера выбираем из Приложения 2).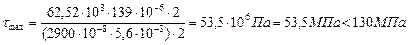 Прочность балки, состоящей из двух швеллеров, по нормальным и касательным напряжениям обеспечена.
Прочность балки, состоящей из двух швеллеров, по нормальным и касательным напряжениям обеспечена.
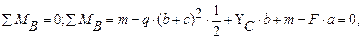

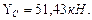
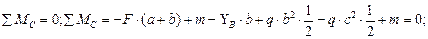
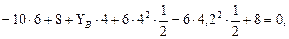
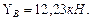
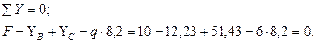
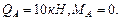
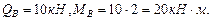
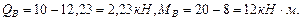
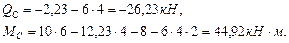
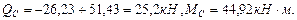
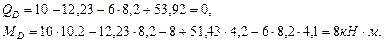
 (рис 4.3),
(рис 4.3),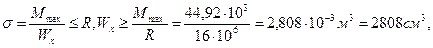

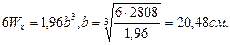
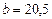 см, тогда
см, тогда 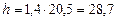 см,
см,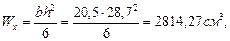
 <16 МПа.
<16 МПа.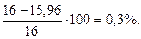
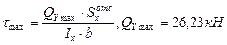 (из эпюры поперечных сил, рис 4.3).
(из эпюры поперечных сил, рис 4.3).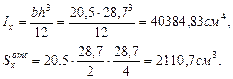


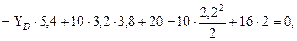
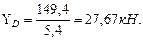
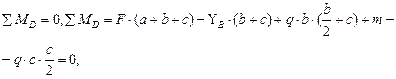
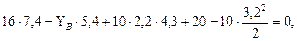


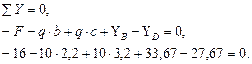
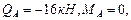

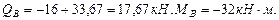

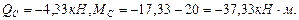
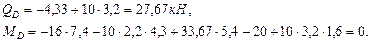
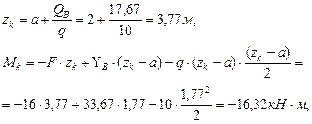
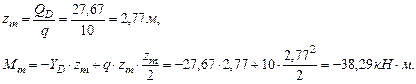
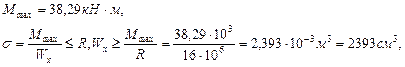
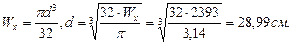
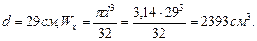
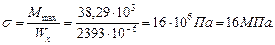
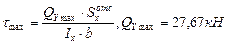 (из эпюры поперечных сил,
(из эпюры поперечных сил,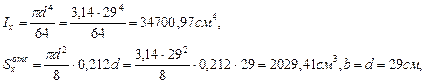
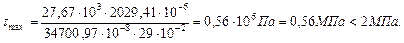 Прочность деревянной балки по нормальным и касательным напряжениям обеспечена.
Прочность деревянной балки по нормальным и касательным напряжениям обеспечена.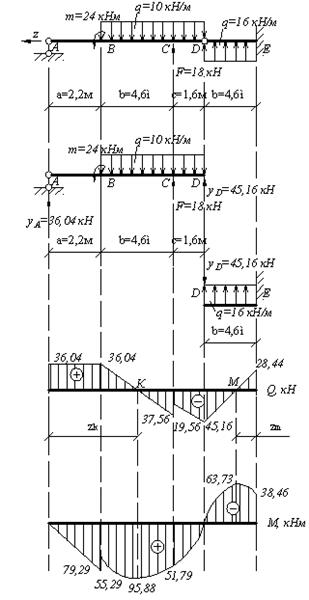
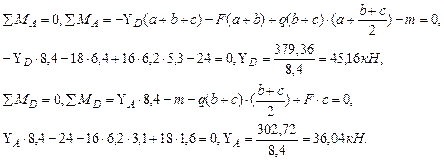 Определим правильность определения опорных реакций:
Определим правильность определения опорных реакций: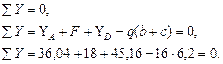
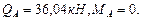
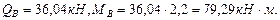
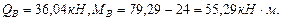
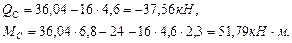
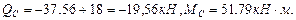
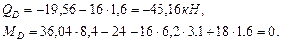
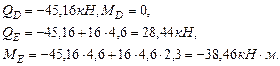
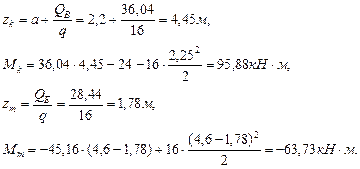
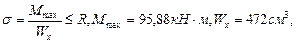

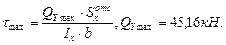
 - все геометрические характеристики двутавра № 30 выбираем из сортамента (Приложение 1).
- все геометрические характеристики двутавра № 30 выбираем из сортамента (Приложение 1).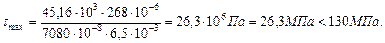
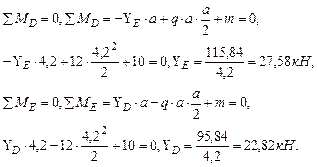

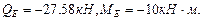
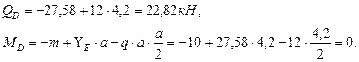
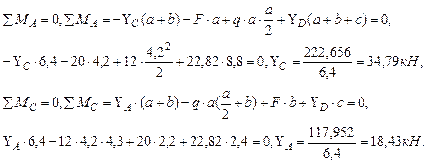 Проверяем правильность определения реакций опор:
Проверяем правильность определения реакций опор:
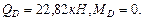
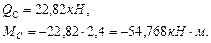
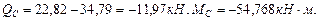


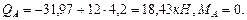
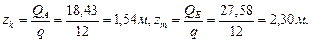
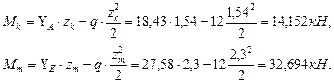
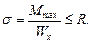 Для двутавра № 24 из сортамента (Приложение 1) выпишем значение момента сопротивления:
Для двутавра № 24 из сортамента (Приложение 1) выпишем значение момента сопротивления: 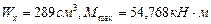 (из эпюры изгибающих моментов, рис.5.6).
(из эпюры изгибающих моментов, рис.5.6).