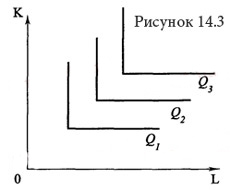
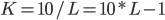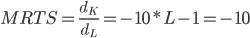Изокванта
Для простоты анализа, как и прежде, будем полагать, что:
Представим в виде таблицы данную функцию для значений
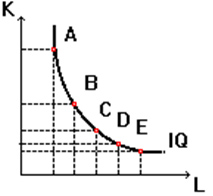
Как видно из таблицы, существует несколько комбинаций труда и капитала, обеспечивающих в определенных пределах заданный объем выпуска. Например Если отложить по горизонтальной оси количество единиц труда, а по вертикальной — количество единиц капитала, затем обозначить точки, в которых фирма выпускает один и тот же объем, то получится кривая, представленная на рисунке 14.1 и называемая изоквантой. Каждая точка изокванты соответствует комбинации ресурсов, при которой фирма выпускает заданный объем продукции. Набор изоквант, характеризующий данную производственную функцию, называется картой изоквант.
Свойства изоквант Свойства стандартных изоквант аналогичны характеристикам кривых безразличия: 1. Изокванта, так же как и кривая безразличия, является непрерывной функцией, а не набором дискретных точек. 2. Для любого заданного объема выпуска может быть проведена своя изокванта, отражающая различные комбинации экономических ресурсов, обеспечивающих производителю одинаковый объем производства (изокванты, описывающие данную производственную функцию, никогда не пересекаются). 3. Изокванты не имеют участков возрастания (Если бы участок возрастания существовал, то при движении вдоль него увеличивалось бы количество как первого, так и второго ресурса). Предельная норма технологического замещения Предельная норма технологического замещения одного ресурса на другой (например, труда на капитал) показывает степень замещения труда капиталом, при котором объем выпуска остается неизменным. Алгебраическое выражение, показывающее степень, в которой производитель готов сократить количество капитала в обмен на увеличение труда, достаточную для сохранения прежнего объема выпуска имеет вид:
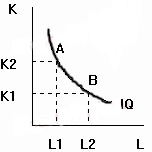
Как видно на рисунке выше, при переходе из точки Сокращение выпуска в результате уменьшения затрат капитала равно произведению Таким образом, можно записать, что Производственная функция, связывающая между собой количество капитала, труда и объем выпуска, позволяет также рассчитать предельную норму технологического замещения через производную данной функции: Это значит, что графически в любой точке изокванты предельная степень технологического замещения равна тангенсу угла наклона касательной к изокванте в этой точке. Пример 14.2 Нахождение MRTS для заданной функции Условие: Пусть производственная функция имеет вид Определить: Решение:
Очевидно, что степень замещения труда капиталом не остается постоянной при движении вдоль изокванты. При перемещении вниз по кривой абсолютное значение MRTS труда капиталом убывает, так как все большее количество труда приходится использовать, чтобы компенсировать снижение затрат капитала (Так, в приведенном выше примере при L=1 MRTS=-10, а при L=10 MRTS=-0.1.) В дальнейшем MRTS достигает своего предела (MRTS=0), а изокванта приобретает горизонтальный вид. Очевидно, что дальнейшее снижение затрат капитала приведет лишь к сокращению объемов выпуска. Количество капитала в точке Е — минимально допустимое для данного объема производства (аналогичным образом минимально допустимое для производства данного объема количество труда имеет место в точке А).
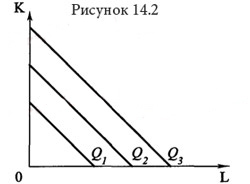
Убывание предельной нормы технологического замещения Убывание MRTS одного ресурса другим характерно для большинства производственных процессов и характерно для всех изоквант стандартного вида. Особые случаи производственной функции (изокванты нестандартного вида) Совершенная взаимозаменяемость ресурсов Если ресурсы, используемые в процессе производства, являются абсолютно заменяемыми, то
Фиксированная структура использования ресурсов Если технологический процесс исключает замещение одного фактора на другой и требует использование обоих ресурсов в строго фиксированных пропорциях, производственная функция имеет вид латинской буквы
Примером подобного рода может служить работа землекопа (одна лопата и один человек). Увеличение одного из факторов без соответствуюещго изменения количества другого фактора нерационально, поэтому технически эффективными будут лишь угловые комбинации ресурсов (угловая точка — точка, где пересекаются соответствующие горизонтальная и вертикальная линии).
|

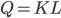
 и
и 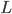 от 1 до 4.
от 1 до 4.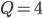 можно получить, используя комбинацию (1,4), (4,1) и (2,2).
можно получить, используя комбинацию (1,4), (4,1) и (2,2).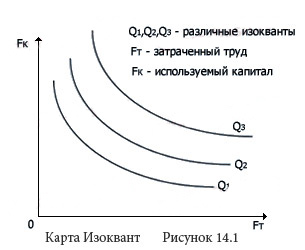
 .
.
 в точку
в точку 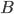 объем производства остается неизменным. Это означает что сокращение выпуска в результате уменьшения затрат капитала
объем производства остается неизменным. Это означает что сокращение выпуска в результате уменьшения затрат капитала 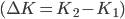 компенсируется увеличением выпуска за счет использования дополнительного количества труда
компенсируется увеличением выпуска за счет использования дополнительного количества труда 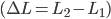 .
. на предельный продукт капитала, или
на предельный продукт капитала, или  . Увеличение выпуска за счет использования дополнительного количества труда в свою очередь равно произведению
. Увеличение выпуска за счет использования дополнительного количества труда в свою очередь равно произведению  на предельный продукт труда, или
на предельный продукт труда, или 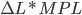 .
.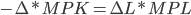 . Запишем данное выражение по-иному:
. Запишем данное выражение по-иному: 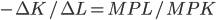 или
или 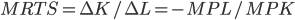 .
. .
.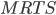 при
при 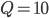 для
для 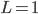 .
.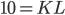 ,
,