Описание используемых стандартных функций.
Стандартные функции, возвращают вещественный результат при вещественном или целом аргументе: · Cos(x), вычисляет косинус аргумента x. · Sin(x), вычисляет синус аргумента x. · Abs(x), вычисляет абсолютную величину аргумента x. Текст программы № 15.а Rem lab1{ вариант №15.a} const x=2.346 dim y:as single Primt “Вычислим значение функции Y=1+cos^2(x)+sin^3(x) при x=2.346” y:=1+x*cos(x)*cos(x)+sin(x)*sin(x)*sin(x) Print “y=”;y Print “Y^2=”;y^2 Print “ABC(Y^2)=”,abs(y^2) end Текст программы № 15.б Rem lab1{ вариант №15.b} const x0=-0.8 const y0=0.9 const r=1 pro:=(x0*x0+y0*y0<=r*r) and ((x0+1<=y0) or (abs(x0)-1>=y0)) Print “Точка с координатами М(',x0:0:1,'.',y0:0:1,')” if pro then Print “Принадлежит заштрихованной области.” else Print “Не принадлежит заштрихованной области.” end Распечатка результатов выполнения программы. Программы № 15.а
Программы № 15.б
Варианты заданий 1) а) Y=sin(x)+x б) Координаты исследуемой точки: (3; 2) Область (I четверть)
2) а) Y= x+ б) Координаты исследуемой точки: (1.5; 0.5) Область (III четверть)
3) а) Y=x б) Координаты исследуемой точки: (0.1; 0.3) Область (квадрат):
4) а) Y= б) Координаты исследуемой точки: (0.6; 2.5) Область (окружность):
5) а) Y= tg x - (5 - x б) Координаты исследуемой точки: (-0.7; 0.2) Область (I и IV четверть):
6) а) Y=25x б) Координаты исследуемой точки: (-0.3; -0.5) Область (III четверть):
7) a) Y= б) Координаты исследуемой точки: (2.5; 3) Область (между окружностью и квадратом):
8) a) Y= б) Координаты исследуемой точки: (-1; -5) Область (вся область определения):
9) a) Y= sin x
10) a) Y= б) Координаты исследуемой точки: (-5; 7) Область (I четверть, ниже диагонали прямоугольника)
11) a) Y= 2 б) Координаты исследуемой точки: (1; -3) Область (I, II, IV четверти):
12) a) Y= б) Координаты исследуемой точки: (-0.5; 0.5) Область (II, IV четверти):
13) a) Y = б) Координаты исследуемой точки: (0.5; 1) Область (вся область определения):
14) a) Y= б) Координаты исследуемой точки: (0.75; -0.75) Область (вся область определения):
15) a) Y=
16) a) Y= arcsin x+x б) Координаты исследуемой точки: (1.5; 0.5) Область (II, IV четверти):
17) a) Y= cos arctg x при х = -0.692 б) Координаты исследуемой точки: (0.2; 0.9) Область (II, III четверти):
18) a) Y= 7 arcctg x б) Координаты исследуемой точки: (0.75; -0.3) Область (II, III, IV четверти):
19) а) Y= 5 x б) Координаты исследуемой точки: (0.2; 0.45) Область (вся область определения):
20) a) Y= 2 б) Координаты исследуемой точки: (0.4; -2.5) Область (I, III, IV четверти):
21) a) Y= б) Координаты исследуемой точки: (0.0; 0.0) Область (I, II, III четверти):
22) a) Y= 1+ б) Координаты исследуемой точки: (1; 1.5) Область (пересечение окружностей):
23) a) Y= ch б) Координаты исследуемой точки: (-0.5; 0.9) Область (I, IV четверти, пересечение oкружности и треугольника):
24) a) Y = arcsin x + x б) Координаты исследуемой точки: (1.5; 0.0) Область (окружность, но не треугольник):
|

 при х = 5.137
при х = 5.137


 Y
5 X
Y
5 X
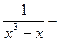 2 при x = 0.675
2 при x = 0.675


 Y
-7
-1 X
Y
-7
-1 X
 - cos arcsin x при х=0.051
- cos arcsin x при х=0.051




 2 Y
-2 2 X
-2
2 Y
-2 2 X
-2
 при х = 7.873
при х = 7.873
 1 Y
-1 1 X
-1
1 Y
-1 1 X
-1

 Y
1 X
-1
Y
1 X
-1
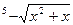 при х = 25.144
при х = 25.144

 Y
-1 X
-1
Y
-1 X
-1
 + ctg arctg x
+ ctg arctg x  при х = -5.113
при х = -5.113




 1 Y
-1 1 X
-1
1 Y
-1 1 X
-1
 при х = 10.237
при х = 10.237


 1 Y
-1 1 X
-1
1 Y
-1 1 X
-1
 при х = 1.031
при х = 1.031 1 Y
-1 1 X
1 Y
-1 1 X
 при х = 11.131
при х = 11.131


 1 Y
2 X
1 Y
2 X
 x cos(x) +1 при х = 34.211
x cos(x) +1 при х = 34.211

 1 Y
-1 1 X
-1
1 Y
-1 1 X
-1
 при х = -12.333
при х = -12.333


 при х = -3.449
при х = -3.449

 1 Y
-1 1 X
-1
1 Y
-1 1 X
-1
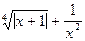 при х = -45.276
при х = -45.276


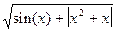 при х = 3.778
при х = 3.778











 5 Y
-5 3 X
-1
5 Y
-5 3 X
-1
 при х = 28.954
при х = 28.954



 при х = 4.741
при х = 4.741



 при х = 2.312
при х = 2.312



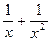 при х = -0.387
при х = -0.387


 при х = 4.352
при х = 4.352


 Y
1 2 X
-1
Y
1 2 X
-1
 -1 1 X
-1
-1 1 X
-1



