Роль противоречивых ситуаций в развитии мышления детей

В детской психологии до сих пор недостаточно исследо­ван вопрос о самостоятельном усовершенствовании дош­кольниками средств и способов мыслительной деятель­ности. Повышение уровня самоорганизации психической

деятельности — одна из основных линий умственного раз­вития детей. Такая «постановка проблемы развития ре­бенка делает чрезвычайно актуальной задачу изучения тех психологических условий, которые благоприятствуют превращению его деятельности, первоначально склады­вающейся под влиянием взрослого, в подлинную детскую самодеятельность» [Н. Н. Поддьяков, 1983, с. 38].

В этой связи нас интересует вопрос о тех внутрен­них условиях, которые позволяют ребенку перестраивать уже имеющиеся у него средства и способы мышле­ния. Данные, показывающие возможность такой пере­стройки, приведены Л. Ф. Обуховой [1972]. На боль­шом экспериментальном материале она поясняет, что необходимо не только формирование нового способа мышления, не менее важно, чтобы ребенок перестроил старый способ решения задачи. Чем глубже происхо­дит перестройка старых способов мышления в связи с формированием новых, тем более гибким оказывается новый способ, тем легче он применяется в новой, незна­комой ребенку ситуации.

Какие же условия заставляют детей изменять средства мышления? Если ребенку в решении новой для него задачи старые способы позволяют получить правильный резуль­тат, у него не появится потребность преобразовывать способы решения задач. Но допустим, ребенок не решил задачу. Тогда у него имеется две возможности: 1) попы­таться преобразовать те способы, которыми он владеет, и все-таки решить задачу, 2) получить дополнительную информацию о том, как решать задачу. В успехе реализации первой возможности у ребенка уверенности нет, в то время как обращение к взрослому гаран­тирует решение.

Следовательно, когда ребенку нужно решить трудную для него задачу, способ решения которой не очевиден, он не всегда стремится преобразовывать средства и спосо­бы мышления. В этих условиях необходимость перестрой­ки старых способов нередко подменяется другой воз­можностью — получить дополнительные знания о решении задачи.

Целесообразно рассмотреть процесс решения дошколь­никами задач в случаях, когда обнаруживается несоот­ветствие известных средств и способов особенностям предложенных задач. Другими словами, важно исследо­вать, как ребенок подходит к необходимости преобразо­вания имеющихся у него средств и способов мышления,

 

если убедится в их непригодности, в их несоответствии поставленной задаче. Мы полагаем, что понимание несоот­ветствия возникает тогда, когда ребенок обнаруживает в ситуации взаимоисключающие свойства и отношения. Ситуации такого типа мы называем противоречивыми. Противоречивая ситуация рассматривается в контексте тех средств, которыми располагает ребенок к моменту вы­полнения задания. Ребенок, применяя определенную систе­му мыслительных средств, и именно благодаря этой систе­ме, устанавливает наличие у предметов взаимоисключаю­щих свойств или взаимоисключающих отношений. Так как интерпретация познавательной ситуации зависит от зна­ний детей, то одно и то же задание может приводить или не приводить к возникновению противоречивой ситуации.

Мы поставили перед собой три исследовательские задачи.

1. Показать возможность возникновения противоречи­вых ситуаций в познавательной деятельности дошколь­ников.

2. Раскрыть основные особенности перестройки средств и способов мышления в ходе преобразования противоречи­вых ситуаций у дошкольников.

3. Показать эффективность применения противоречи­вых ситуаций в формировании новых психических обра­зований.

Несмотря на то что вопрос о роли противоречивой ситуации в познавательной деятельности дошкольника специально в психологии не рассматривался, в неко­торых исследованиях можно встретить данные, имеющие к нему прямое отношение. А. В. Запорожец, Г. Д. Луков [Психология детей..., 1964] показали, что дошкольники в ряде случаев могут осознавать противоречивость своих суждений. Представляют интерес некоторые экспе­риментальные ситуации, примененные в исследовании А. А. Венгер [1959]. В одном из заданий детям показы­вали, как шарик скатывается с поверхности кубика. Затем шарик крепился с помощью гвоздя к кубику так, чтобы ребенок этого не видел. Дошкольники должны были объяснить причину падения шарика в первом случае и отсутствие падения во втором.

Особенность этой экспериментальной ситуации, на наш взгляд, заключается в том, что ребенок сталкивается с взаимоисключающими свойствами шарика: „падает" и „не падает". Данная ситуация фактически противоречива.

Необходимость интерпретации, т. е. необходимость дать ответ, какое же из свойств шарика является „пра­вильным", побуждает ребенка исследовать ситуацию и определить причину, удерживающую шарик на наклонной плоскости.

В исследовании А. В. Запорожца и Г. Д. Лукова и в исследовании А. А. Венгер был сделан сходный вывод, что дошкольники могут дать правильные ответы в ситуациях, с которыми они ранее были хорошо знакомы. Отсюда следует, что дошкольники оказываются способными обнаружить причину противоречивости ситуа­ции, если они ранее сталкивались с подобными ситуация­ми. Рассмотрим этот вопрос более подробно.

В качестве наиболее доступного средства отражения ситуации дошкольниками, как известно, выступает образ. Однако противоречие может быть отражено в образном плане только в том случае, если взаимоисключающие стороны „схвачены" ребенком одновременно. В ситуации с шариком ребенок должен одновременно отражать и то, что шарик падает, и то, что шарик не падает. Следовательно, ребенок должен актуализировать сразу два образа ситуации, каждый из которых отражает одну из ее противоречивых сторон. Подобное отражение воз­можно, если ребенок хорошо знаком с ситуацией. В этом случае у него существует представление о том, какой должна быть ситуация, и это представление „накла­дывается" на перцептивный образ ситуации, отражающий то, какова ситуация в данный момент. Тогда сличение прошлого опыта, фиксированного в представлении, с противоречащим ему перцептивным образом ставит дош­кольника перед противоречивой ситуацией, а необхо­димость действовать в ней заставляет искать причину несоответствия.

Первые представления о предметах начинают форми­роваться у детей в раннем возрасте. Мы предположили, что простейшие противоречивые ситуации могут возни­кать тогда же.

Для проверки была разработана несложная методика. Детям раннего возраста предлагалась хорошо знакомая игрушка „мишка-каталка". На колесо игрушки надевалась резинка так, что колесо не крутилось, а перемещение игрушки затруднялось. Ребенка просили поиграть с иг­рушкой. В эксперименте* сначала участвовали 15

* Эксперимент выполнен совместно с М. А. Фарбер

 

детей раннего взраста, затем один ребенок выбыл. В зависимости от характера действий было выделено 3 группы детей. В I группу вошли 5 малышей. Они не заметили изменений игрушки и действовали, как обычно, т. е. как если бы колеса каталки свободно вращались. Один ребенок (Дима М.) на вопрос экспе­риментатора: „Крутятся ли колеса?"— ответил утверди­тельно.

Во II группу также вошли 5 детей. Они заметили, что игрушка не перемещается. Как правило, они удивля­лись, находились в замешательстве, говорили „не едет". Однако причину, по которой движение было затруднено, они не нашли. В качестве примера приведем ответ Саши Т. Когда он заметил, что каталка не едет, сказал: „Папа придет, будет едет".

В III группу вошли 4 ребенка. Все они отметили, что каталка „не едет". Далее трое молча указали пальцем на резинку, а один не только показал пальцем на резинку, но и сказал: „Эта мешает".

Данные этого эксперимента показывают, что уже в раннем возрасте дети могут в знакомых ситуациях пони­мать простейшие причинные отношения. Однако нас эти результаты интересуют с другой точки зрения. Они свидетельствуют о том, что ребенок способен устано­вить несоответствие между репродуктивным образом хо­рошо знакомого предмета и его перцептивным образом, т. е. между тем, каким предмет был и каков он есть. Ответ „не едет" указывает на то, что ребенок ожидал противоположного эффекта. Иными словами, возникла противоречивая ситуация.

Особенность такой ситуации определялась тем, нас­колько у ребенка был сформирован репродуктивный образ игрушки и развита ориентировочно-исследовательская деятельность. Действия детей I группы показывают, что противоречивая ситуация у них не возникала как из-за несформированности представления, так и из-за неразвитости ориентировочно-исследовательской деятель­ности. У детей II группы представления в известной мере были сформированы, что и приводило к возникнове­нию противоречивых ситуаций. Но недостаточное разви­тие ориентировочно-исследовательской деятельности не позволяло малышам установить причину, затруднявшую перемещение игрушки. У детей III группы и представ­ления и ориентировочно-исследовательская деятельность были достаточно сформированы для того, чтобы у

них не только возникла противоречивая ситуация, но и была преобразована.

Сопровождалось ли преобразование значительными из­менениями в мышлении детей? Вероятнее всего, нет. В представлениях детей существенные моменты ситуации отражались правильно уже до ее преобразования. Преодоление же противоречивости ситуации фактически было ограничено анализом наглядного, перцептивного плана опять-таки в соответствии с исходным представле­нием. Поэтому подобные ситуации мы назвали нагляд­ными противоречивыми ситуациями.

На наш взгляд, в исследовании мышления дошколь­ников большой интерес представляют противоречивые ситуации, в которых оба противоречивых образа- не отра­жают существенных свойств ситуации. Можно предпо­ложить, что в этом случае ребенок будет вынужден отказаться как от первого, так и от второго образа ситуации и построить некоторый третий, который бы снял противоречивость ситуации. Такие ситуации мы назвали противоречивыми ситуациями со скрытыми существенными свойствами.

Если наглядные противоречивые ситуации сравнитель­но часто встречаются в повседневной практике дошколь­ников, то противоречивые ситуации со скрытыми сущест­венными признаками — реже. Мы разработали методику „коробка с грузом", которая была направлена на то, чтобы поставить дошкольников перед противоречивой ситуацией со скрытыми существенными свойствами*. Она включала 2 ситуации.

Экспериментальная ситуация 1. Ребенку предъявлялся пустоте лый прямоугольный параллелепипед (дети обычно называли его „кубик"). Внутри его находился свободно перемещавшийся груз. Наклон параллелепипеда в сторону вызывал соответствующее перемеще­ние груза и, следовательно, смещение центра тяжести всей системы.

Экспериментатор не раскрывал особенностей внутреннего строе­ния параллелепипеда. Он показывал его ребенку на расстоянии 2—3 м. Придерживая рукой, экспериментатор располагал его на столе так, чтобы большая часть параллелепипеда выступала над краем стола. Предварительно груз внутри перемещался так, чтобы в этом положении параллелепипед не падал. Продолжая удерживать его рукой и создавая тем самым иллюзию падения, экспериментатор задавал ребенку вопрос: „Что будет с кубиком, если я перестану его держать?" Дальнейшие действия экспериментатора зависели от ответов детей. Как правило, дети говорили, что кубик упадет. В

* Нас интересуют только противоречивые ситуации со скрытыми существенными свойствами, в дальнейшем будет кратко называть их «противоречивые ситуации».

 

этом случае экспериментатор поднимал руку и обращал внимание ребенка на то, что кубик не упал. Затем экспериментатор брал кубик в руки и спрашивал ребенка: „Что будет с кубиком, если я опять положу его точно так же и не буду держать? Кубик упа­дет или нет?" Если ребенок говорил „не упадет", эксперимен­татор, прежде чем поставить кубик на край стола, вызывал нак­лоном кубика смещение центра тяжести и, отпуская кубик, пока­зывал его падение. Каждый раз, действуя подобным образом, экс­периментатор в зависимости от ответа располагал груз внутри кубика так, чтобы показать ребенку несоответствие его предска­зания реально наблюдаемой картине. Процедура прекращалась, если ответы детей не менялись.

Экспериментальная ситуация 2. Ребенку предъявлялся картонный цилиндр. К его внутренней поверхности крепился груз. Бла­годаря этому цилиндр можно было поставить на наклонную плос­кость так, что он либо поднимался вверх, либо скатывался вниз. Ребенок должен был ответить на вопрос: „Куда покатится колесо?" Порядок проведения эксперимента был точно таким же, как и в ситуации 1.

Если предположить, что дошкольники, по крайней мере, на начальном этапе интерпретируют действитель­ность в наглядно-образном плане, тогда предложенные нами экспериментальные ситуации обладали для детей скрытыми свойствами: объекты имели сложное внутреннее строение, которое в наглядном плане не было пред­ставлено. Кроме того, сам характер предъявления был та­ков, что в пределах наглядного плана объекты обладали взаимоисключающими свойствами: „падает — не падает", „спускается — поднимается". При этом противоречивые образы, в которых фиксировались взаимоисключающие свойства предметов, не могли отражать существенные моменты ситуации. Таким образом, в нашем экспери­менте создавались условия для возникновения противо­речивой ситуации.

В эксперименте участвовали дошкольники трех воз­растных групп детского сада: средней, старшей и подго­товительной (по 15 детей в каждой). При 1-м предъяв­лении параллелепипеда дети трех групп отвечали сходно:

одни говорили „упадет", „сломается", „разобьется", неко­торые молчали. При 2-м предъявлении, после того как они увидели, что кубик не упал, большинство детей утверждали „не упадет". В дальнейших предъявлениях, когда дети увидели и то, как кубик падал, и то, как он оставался на столе, были обнаружены различные стратегии ответов детей.

Стратегия 1. Ребенок дает ответ на основании того, что он увидел в предыдущем предъявлении. Так, если

дошкольник наблюдал падение, он говорил, что кубик упадет. Но уже в следующем предъявлении, когда оказывалось, что кубик не падал, ребенок говорил „не упадет".

Стратегия 2. Ребенок повторяет что-либо одно: „упа­дет" или „не упадет".

Стратегия 3. Сначала ребенок говорит, например, „упадет", а затем быстро говорит „не упадет", потом опять — „упадет", тут же говорит „не упадет" и т. д. Ребенок как бы не решается выбрать окончательный вариант.

Стратегия 4. Ребенок говорит, что он не знает, упа­дет кубик или нет, так как он „и падает, и не падает".

Стратегия 5. Ребенок дает различные, в том числе правильные, объяснения свойств кубика.

Ответы в экспериментальной ситуации 2 по характеру были такими же, как и в ситуации 1, поэтому специально они рассматриваться не будут.

Наибольший интерес представляют действия детей средней группы. Девять из них в ответах использовали стратегии 1 и 2. Ответы детей указывают на то, что они не могли соотнести репродуктивный и перцептив­ный образы между собой: один из них вытеснялся дру­гим. Шесть детей применили стратегию 3. Внешне поведе­ние дошкольников напоминало угадывание одного из от­ветов „упадет" или „не упадет". При этом они коле­бались и долго не могли решиться на окончательный ответ. Эти действия, на наш взгляд, принципиально от­личались от ответов, которые соответствовали стратегии 1 или стратегии 2. Колебания ребенка явно указывали на отражение им в плане представлений двух возможнос­тей в состоянии кубика. Иными словами, из двух образов, один из которых отражал, что кубик „падает", а другой — что кубик „не падает", у дошкольника возникал слож­ный образ, включающий оба варианта. На его основе ребенок и должен был дать ответ. Но этот сложный образ, построенный из двух наглядных образов, которые не отражали существенных свойств кубика, не позво­лял ребенку дать правильный ответ. Говоря, например, „упадет", ребенок легко обнаруживал частичность ответа, поскольку образ включал и второе состояние кубика — „не упадет". Но как только дошкольник восполнял эту часть, т. е. говорил „не упадет", он опять-таки давал частичный ответ, теперь уже терялась другая часть образа. Поэтому, чтобы сохранить полноту образа, ребе-

 

нок вынужден был не останавливаться на каком-то ва­рианте, а постоянно переходить от одного ответа к друго­му.

Подтверждение такой интерпретации стратегии 3 мы встретили в другом эксперименте, проведенном с другим контингентом дошкольников. Мы предлагали им на пер­вый взгляд несложное задание. В групповой комнате детского сада на некотором расстоянии друг от друга на стульчиках располагались три большие куклы. Каждая кукла сидела на своем стульчике. Ребенку давали кор­зиночку, в которой лежали три кубика. Ребенка просили „сделать так, чтобы у каждой куклы было по кубику и один кубик при этом остался в корзинке". Правильное выполнение задания заключалось в том, чтобы ребенок двум куклам положил по одному кубику, а третьей — кубик вместе с корзинкой.

Выполнение задания вызвало у детей трудности. Боль­шинство из них говорили, что „не хватает одного кубика", что „кубик нужно распилить" и т. д. Но были и такие дети, который действовали следующим образом. Ребенок брал первый кубик, клал его кукле. Второй кубик ребенок оставлял в корзинке на столе. А третий кубик ребенок держал в руке и постоянно переносил его от одной куклы, оставшейся без кубика, к другой кукле, также оставшейся без кубика. Действия ребенка напо­минали маятник: он все время перекладывал кубик. Таким образом, и в этом случае мы встречаемся с этой своеобразной попыткой устранить противоречивость путем постоянного перехода от одного альтернативного дейст­вия к другому.

Отмеченные особенности действий детей средней груп­пы в соответствии со стратегией 3 позволяют рассмат­ривать их как показатель того, что дошкольники отра­зили противоречивость ситуации. У них возник синтези­рованный образ, согласно которому предмет обладает взаимоисключающими, противоречивыми свойствами. При этом образ не отражал скрытых, существенных особен­ностей предмета, что не позволяло использовать его как основу для адекватной ориентировки в эксперименталь­ной ситуации. Поэтому, если ребенок рассчитывал дать правильный ответ, он в конце концов должен был отка­заться от ориентировки на основе этого образа и попы­таться каким-либо способом его перестроить, изменить.

Дальнейшие ответы детей позволили проследить преоб­разование этого образа. Два ребенка отказались от

эксперимента, четыре дошкольника после ряда предъяв­лении стали говорить, что кубик „н падает и не падает" (стратегия 4). Ответы детей показали, что дошколь­ники не только отразили противоречивую ситуацию в плане образа, но и осознали наличие у предмета двух взаимоисключающих свойств „падает — не падает".

Мы попытались понять роль осознания противо­речивости ситуации в развитии познавательной деятель­ности ребенка и особенности самого процесса осознания. На наш взгляд, осознание противоречия связано прежде всего с установлением субъектом факта несоответствия средств, применяемых для отражения объекта, свой­ствам этого объекта. Ребенок должен не только констатировать, что свойства объекта непредсказуемы однозначно в выбранной системе средств, но и сделать вывод о непригодности средств для данного объекта. Ситуация внешне была предельно наглядной, знакомой ребенку. Поэтому ее первичная интерпретация проходила в рамках привычных (наглядных) знаний ребенка о неживой природе. Однако именно обычные представле­ния ребенка о неживой природе, в частности о внутрен­ней однородности кубиков, и оказались неадекватными в данном случае. Перед ребенком встает проблема: или надо искать другую, необычную систему средств, или вообще отказаться от попыток предсказания поведения предмета, поскольку прежние способы уже заведомо не­пригодны. В этот момент, т. е. в момент оценки старой системы средств, и возникает противоречивая ситуация. Ее специфика заключается в том, что познавательная дея­тельность ребенка становится пристрастной: она направ­ляется уже на то, чтобы не только отразить свойства объекта, но и отразить их непротиворечиво.

Эта деятельность может развертываться в трех нап­равлениях: как недеяние, отказ от деятельности, т. е. универсальное разрешение всех противоречий; как пере­стройка системы интерпретации свойств объекта; как более детальное обследование объекта с целью выделения в нем новых, существенных свойств.

Как было отмечено, два ребенка средней группы отказались участвовать в эксперименте после достижения стратегии Э. В этом случае мы столкнулись с вопросом о переходе операциональных компонентов мыслительной деятельности в мотивацргсятные. Отказ от выполнения задания можно рассматривать и как показатель недоста­точной сформированности познавательной направленности

 

личности и как найденный ребенком универсальный вариант разрешения противоречивой ситуации.

Три ребенка средней группы, после того как отметили, что кубик „и падает и не падает", сказали: „он волшеб­ный". В известном смысле они нашли звено, опос­редствующее противоречивые свойства объекта, и выра­зили его словом „волшебный" (стратегия 5). Это опосредствование показало, что мыслительный процесс вышел за рамки экспериментальной ситуации. Строго говоря, детям не задавался вопрос „почему?", формально ребенок должен был лишь сказать „упадет" или „не упадет". Обращение к представлениям, лежащим вне наглядных особенностей ситуации, свидетельствовало, что возникла особая мыслительная деятельность, направ­ленная на замену средств, с помощью которых осущест­влялось отражение ситуации. Ребенок должен был пере­смотреть свой опыт. В этом случае мыслительная дея­тельность обратилась на себя, т. е. приобрела выра­женный рефлексивный характер. Познавательная деятель­ность детей была направлена не только на поиск адекватных определений, но и на выявление скрытых особенностей ситуации с целью объяснения ее противо­речивости. Вот как объяснил этот процесс ребенок средней группы, после того как понял, что не может точно сказать, что будет с кубиком: „Сначала я не видел. А потом последний раз сообразил. Я видел, как вы наклонили коробку. Там что-то зашуршало. Оно пере­мещается. Коробка утяжеляется". Таким образом проти­воречивая ситуация заставила ребенка изменить средства отражения ситуации, проникнуть за внешнюю видимость вещи и понять ее внутреннее строение.

Ответы старших дошкольников в основном были такими же. Три ребенка дали ответы, основанные на стратегиях 1 и 2, а 12 — на стратегии 5.

Результаты детей подготовительной группы характери­зовались быстрым достижением адекватного объяснения и большим разнообразием. Они говорили: „кубик приклеен", „там магнитик", „внутри что-то есть".

Анализируя ответы детей, можно сделать следующие выводы.

1. В эксперименте у дошкольников возникали противо­речивые ситуации.

2. В ходе их преобразования наблюдался процесс движения мышления ребенка, характеризовавшийся опре­деленным порядком смены стратегий ответов детей с

общим для всех возрастных групп направлением:

1; 2-^3^4-^5.

3. В процессе мышления дети дошкольного возраста выходили за пределы чувственно воспринимаемых свойств ситуации, раскрывали внутреннее строение вещей. При этом происходила перестройка первоначальных представ­лений детей о ситуации.

4. Причина движения мышления ребенка, связанная с перестройкой мыслительных средств, в которых отра­жались экспериментальные объекты, была обусловлена противоречивыми ситуациями, которые формировались в эксперименте.

5. Противоречивые ситуации способствовали развер­тыванию рефлексивной мыслительной деятельности детей в направлении поиска опосредствования противоречия, перестройки системы объяснений. Роль противоречивых ситуаций заключалась также в ориентировании позна­вательной деятельности детей на пристрастный анализ ситуации, на выделение в ней таких особенностей, которые помогали раскрыть ее противоречивость.

6. Наметились следующие звенья процесса образова­ния противоречивых ситуаций: отражение в образном плане противоречивых ситуаций без отражения сущест­венных свойств; синтезирование сложного образа, отра­жающего наличие в ситуации взаимоисключающих свойств и отношений предметов; осознание противоречи­вой ситуации, т. е. уяснение объективности существования взаимоисключающих свойств и отношений, а следователь­но, уяснение невозможности однозначно предсказать из­менения ситуации на основе созданного образа; осозна­ние непригодности выбранной системы интерпретации ситуации из-за невозможности ее адекватного приме­нения; возникновение противоречивой ситуации как необ­ходимости заменить, перестроить систему средств, с помощью которых первоначально отражалась ситуация.

Таким образом, результаты эксперимента позволяют рассматривать противоречивую ситуацию в качестве еще не изученного условия развития мышления дошкольников.

Рассмотрение противоречивых ситуаций в качестве внутренних психологических условий движения мышления дошкольников подводит к постановке целого ряда вопро­сов. Один из них связан с пониманием развития образного мышления, представленным в работах Ж. Пиа­же. Развитие образного мышления Ж. Пиаже видел прежде всего в способности детей строить предвосхищаю-

 

щие образы. Изучая поведение детей в изменяющихся ситуациях, т. е. таких, которые объективно характеризуют­ся различными начальными и конечными состояниями, Ж. Пиаже выделил два класса образов: репродуктивные и предвосхищающие. Под предвосхищающим образом он понимал образ измененной ситуации при условии, что эти изменения ранее не были восприняты ребенком [Л. Р1аое1, В. ЛпЬеМег, 1961].

Ж. Пиаже отмечал, что формирование предвосхищаю­щего образа предполагает построение в мыслительном плане непрерывной картины изменений начального состоя­ния ситуации. Поэтому, указывал он, умение ребенка строить предвосхищающие образы определяется уровнем развития его интеллектуальных операций, по отноше­нию к которым образ выступает как материал логических преобразований. Тем самым развитие образного мышле­ния в концепции Ж. Пиаже фактически отрицается, поскольку оно оказывается лишенным своих внутрен­них движущих сил.

Мы не можем согласиться с подобным заключением. Оценивая перспективы развития образного мышления детей, Ж. Пиаже не учитывал две важные возможности:

1) как было показано в нашем эксперименте, противо­речивая ситуация выступает как внутреннее условие развития собственно образного мышления; 2) кроме того, развитие образного мышления происходит при формирова­нии предвосхищающих образов на основе репродуктив­ных без построения непрерывной картины изменен-ий си­туации, отражающей переход из одного состояния в Другое.

Для исследования второй возможности развития об­разного мышления мы обратились к представлениям дошкольников, отражающим временные и пространствен­ные отношения.

Анализируя работы отечественных и зарубежных пси­хологов, посвященные особенностям развития представле­ний детей о времени и пространстве, почти в любом фун­даментальном исследовании можно обнаружить факты, которые прямо или косвенно указывают на тесную связь отражения детьми пространственных и времен­ных отношений предметов и явлений. Возникает вопрос, являются ли отмеченные особенности пространственных и временных представлений детей случайными, или за ними стоят еще не исследованные психологические закономерности. Мы исходили из второго предположения.

Была выдвинута гипотеза, что наряду с пространст­венными и временными представлениями, в которых мир отражается расчлененно, у детей существует особая группа пространственно-временных представлений, отра­жающих объективную связь временных и пространствен­ных отношений действительности. Мы полагали, что такие представления играют существенную роль в ориен­тировке дошкольника при решении задач, направленных на выявление связи временных и пространственных отно­шений предметов. Иными словами, подобные пред­ставления при определенных условиях должны выпол­нять функцию предвосхищения.

Экспериментальное изучение поведения ребенка в по­добных условиях было осуществлено Ж. Пиаже [1969]. Он исследовал развитие понятий детей о времени, прост­ранстве и скорости. Однако проблему овладения детьми взаимосвязью временных и пространственных отношений объектов Ж. Пиаже не анализировал, что в значитель­ной степени повлияло на его интерпретацию экспери­ментальных результатов.

По мнению Ж. Пиаже, у дошкольников отсутствуют адекватные понятия о времени и скорости. С подобным заключением трудно согласиться. В ряде ситуаций дошкольники могут адекватно отражать временные отно­шения последовательности, длительность и скорость [ И. С. Фрейдкин, 1972].

Возникает вопрос, почему в одних ситуациях дош­кольники правильно характеризовали временные отноше­ния, а в других — ошибочно. Мы полагаем, что в экспериментах Ж. Пиаже дошкольники отвечали ошибоч­но вследствие того, что ситуация „провоцировала" ребенка ориентироваться на основе образов, в которых времен­ные и пространственные отношения предметов были связа­ны. Причем в этих представлениях не был отражен постепенный переход от начальной ситуации к конеч­ной.

Действительно, ситуации были построены так, что в ходе наблюдений (за движением машинок или напол­нением сосудов) внимание ребенка фактически обра­щалось не на искомые временные показатели, относитель­но которых явления были как раз уравнены, а на другие параметры, которые претерпевали значительные видимые изменения. Ребенок был поставлен в особые условия: он должен был отвлечься от параметров, изменение которых носило ярко выраженный характер, и следить за пара-

 

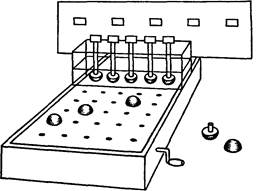
метрами, которые оставались неизменными. Однако имен­но эту задачу в процессе наблюдения за движением машинок перед детьми не ставили. Вопросы задавались только после того, как движение прекращалось и ребенок видел лишь статичную картину, пространствен­ные отношения объектов которой резко отличались друг от друга.

Характеризуя в этих условиях временные отношения, дошкольники опирались на представления о связи временных и пространственных отношений объектов, кото­рые были сформированы к моменту проведения экспе­римента. Подобные представления мы относим к группе пространственно-временных представлений.

Для подтверждения гипотезы о возможности отраже­ния связи временных и пространственных отношений объектов дошкольниками в пространственно-временных представлениях в первую очередь необходимо было установить, имеет ли ориентировочно-исследовательская деятельность дошкольников, направленная на выявление связей такого типа, свою специфику: отличается ли она от отражения временных и пространственных особенностей ситуации в отдельности.

Решение поставленной задачи было связано с выбо­ром таких условий эксперимента, при которых поведение ребенка обусловливается отражением в представлениях связей временных и пространственных отношений объек­тов ситуации. С этой целью мы обратились к динамичным ситуациям, в которых пространственные отношения объек­тов взаимно-однозначно связаны с их временными отношениями. Подобная взаимосвязь возникает при меха­ническом взаимодействии объектов. Действительно, если система объектов в процессе своего движения вступает в механическое взаимодействие с другими объектами, то некоторые стороны этого взаимодействия, в частности его последовательность, будут обусловлены особенностями пространственного расположения элементов системы.

Устройство, в котором пространственное расположение объектов определяет последовательность их взаимодей­ствия, можно рассматривать как модель некоторого вида связи временных и пространственных отношений действи­тельности. Подобное экспериментальное устройство было применено в нашей работе (рис. 1).

Установка состояла из двух групп взаимодействующих объек­тов. Одну группу составляли 5 вертикально расположенных стерж-

ней, которые подвижно крепились на линейной планке. Любой стер­жень мог подниматься вверх на 1,5 см. На каждом стержне была жестко закреплена картинка с изображением животного. Картинки были одинаковы по размерам и различались по содержанию. Если установка находилась в исходном положении, картинки располагались на одном уровне. Другую группу взаимодействующих объектов составляли 5 одинаковых по величине и форме шашек. Шашки располагались на квадратной подвижной плоскости, в которой симмет-

Рис. 1. Общий вид установки, использованной в констатирующем экспе­рименте.

рично были проделаны 5х5 отверстий. В каждое из отверстий можно было легко вставить или вынуть любую из шашек. Вращением ручки осуществлялось поступательное движение плоскости с шашками в направлении к стержням с картинками. Шашка, вставленная в отверстие плоскости, во время движения обязательно проходила строго под центром одного из стержней и, задевая нижнее окончание стрежня, приподнимала его на 1,5 см. От расположения шашек на плоскости зависел порядок их взаимодействия со стержнями, а следовательно, и порядок подъема закрепленных на стержнях картинок. Таким образом, на экспериментальном устройстве моделировалась связь вре­менных и пространственных отношений динамичной ситуации: очеред­ность подъема картинок (временные отношения) зависела от расположе­ния шашек на плоскости (пространственные отношения).

После ознакомления ребенка с установкой, ему предлагали ре­шить 5 задач. Ребенок должен был еще до движения плос­кости расположить на ней шашки так, чтобы потом, когда плоскость придет в движение, приподнялась не одна какая-либо картинка, а все 5, притом в определенной последовательности. Для каждой задачи последовательность выбиралась с таким расчетом, чтобы картинки приподнимались по очереди, одна за другой. Чтобы ребенок помнил последовательность, перед ним за установкой вы­страивался другой, эталонный ряд точно таких же картинок, как и на рабочем ряду. Их пространственное расположение слева напра­во соответствовало заданной последовательности подъема картинок.

3 Н. Н. Поддьяков, А. ф, Говоркова

 

В отличие от положения картинок рабочего ряда на стержнях, в зависимости от задания пространственное расположение картинок эта­лонного ряда менялось. Каждая задача предъявлялась до 10 раз.

Так как проверка правильности расстановки шашек на плоскос­ти была отставлена во времени от процесса ее построения, прави­льное решение задачи было возможно только в том случае, если дошкольники отражали связь временных и пространственных отношений в плане представлений. Другими словами, задача могла быть решена если дети строили правильный предвосхищающий образ.

В эксперименте участвовали 60 детей четырех воз растных групп детского сада, по 15 детей в каждой. Проведенный эксперимент позволил выделить различные уровни решения предъявленных задач.

На I уровне находились дошкольники младшей группы детского сада. Ни один ребенок не решил ни одной задачи. Без специального обучения дети младшей группы выде­ляли только пространственные отношения и не отражали последовательности взаимодействия подвижных и непод­вижных объектов, т. е. временные отношения. В целом их ориентировка в динамичной ситуации носила характер ориентировки в пространстве.

На II уровне находились дети средней группы детско­го сада. Как показал экспер